| Vocademy |
Ohm’s Law
Henry Cavendish, best known for discovering hydrogen and measuring the Earth's density, first described the concept of electrical resistance. His methods were crude. For example, he measured electrical effects by the perceived power of sparks or the strength of electric shocks to his body using various lengths of wire (using Layden jars as power sources). Nevertheless, he determined that longer wires diminished the effects of electricity. Cavendish's work was unpublished and unknown until James Maxwell discovered his writings in the 19th century.
Other experimenters like André Ampère used more precise instruments, such as the torsion balance (a delicate, primitive current meter), to look for the relationship between what we today call voltage, resistance, and current. It was logical to expect that doubling the length of a wire would reduce the current by 50 percent. However, Ampère (and probably others) found that doubling the length of the test wire reduced the current by less than 50 percent. He thus concluded that the effect of resistance on current was logarithmic.
In the 1820s, Georg Ohm, a German physicist, mathematician, and teacher (at the level that we would today call high school) performed his own experiments on the relationship between voltage, resistance, and current. He used a thermocouple[1] immersed in ice water as a precise source of electromotive force. He measured current with a torsion balance galvanometer. This is a magnetic needle (a compass needle) suspended over a wire such that the magnetic field surrounding the wire tries to align the needle perpendicular to the wire. The wire suspending the needle resists the rotation of the needle such that the position of the needle corresponds to the current in the wire. For accuracy, the needle is observed with a microscope. Ohm discovered that if he accounted for the inherent resistance of the thermocouple, applying it in series with the source of electromotive force and adjusting the length of his test wires accordingly,[2] doubling the resistance resulted in half the current.
 |
|
|
When Ohm published his findings in 1827, the scientific community had already accepted a non-linear relationship between resistance and current. As such, Ohm's findings were largely rejected. He eventually resigned his teaching post because of lack of support for his research. Ultimately, Hermann von Helmholtz and others verified Ohm's discovery and Ohm was awarded the Copley Medal by the Royal Society in 1841. Of course, now, the unit of resistance is named after him.
According to legend, André Ampère was so outraged when Ohm published his findings that Ampère contacted Ohm's employer and had him fired from his teaching job. There is no historical evidence that the scientific community took Ohm seriously enough to afford any animosity. His theories, when not simply brushed aside as amateurish, were dismissed as too theoretical and impractical to be of any use. There is no record that Ohm and Ampère had any interaction whatsoever.
Ohm's testing apparatus
The modern version of Ohm's law states, "The ohm is the electric resistance between two points of a conductor when a constant potential difference of 1 volt, applied to these points, produces in the conductor a current of 1 ampere, the conductor not being the seat of any electromotive force." — NIST Special Publication 330, 2019 Edition, Appendix 1.
Not being the seat of any electromotive force means that the test resistance must not produce any electromotive force on its own accord; the electromotive force applied to the test resistance must come from outside the resistance. For example, Ohm's law cannot be applied directly to a battery. This is because the battery produces electromotive force and is therefore "the seat of electromotive force." As Ohm discovered, the resistance inherent in the battery must be applied in series with the source of electromotive force to be valid. Since it is impossible to separate the inherent resistance from the source of electromotive force in a battery, placing a voltmeter across a battery to validate Ohm's law will produce invalid results by definition. You will learn more when we cover Kirchhoff's Voltage Law and Thevenin's Theorem.
Originally, Ohm's Law accounted for all components in the test circuit. Therefore, E represents the total electromotive force supplied by the power source (voltaic pile, thermocouple, etc.). Subsequently, the inherent resistance of the power source must be accounted for in the formula. The following is Ohm's original equation, where R represents the test resistance and r represents the inherent resistance of the power source.
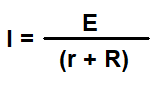 |
The modern version of Ohm's law uses the voltage remaining after the voltage drop across the inherent resistance of the power source. In other words, Ohm accounted for the entire electromotive force of the test circuit, where today, we only account for the voltage applied directly across the test resistance. Therefore, the modern version of Ohm's Law is:
Where:
I = current (amperes)
R = resistance (ohms)
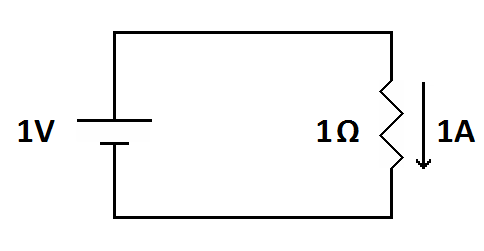
| 1 volt will drive 1 ampere of current through a 1-ohm resistor. |
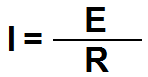 |
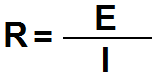 |
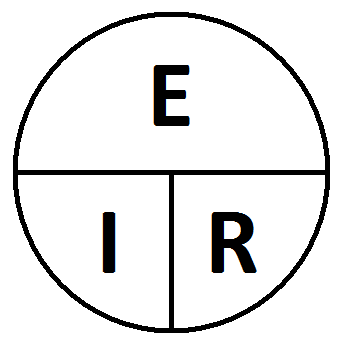
| Ohm's Law circle |
Voltage vs electromotive force
It is popular in some circles to express Ohm's law as V = I R, substituting V (volts) for E (electromotive force). Expressing Ohm's Law with V is arguably more appropriate. If it weren't for E being long established as the preferred symbol, I would probably jump on the V-for-volts bandwagon. Voltage and electromotive force, although both expressed in volts, are not the same. Electromotive force is the energy per unit charge available in the seat of said electromotive force, equivalent to the joules per coulomb available at the source. We will see later that you can have electromotive force (an impetus moving electrons) with no measurable electrical pressure differential (voltage). For example, a changing magnetic field will induce an electrical current in a loop of wire, assuming that the loop of wire is embedded in the magnetic field in the proper orientation. The changing magnetic field imposes an electromotive force on the free electrons in the wire loop, causing electrical current. However, a voltmeter will measure no voltage between any two points on that loop (assuming the loop has uniform resistance).
Voltage will only occur if there is a concentration of resistance (such as a resistor) or a gap in the loop. The foregoing will cause the electrons to bunch up, causing electrical pressure, just as forcing air molecules to bunch up causes air pressure. Therefore, voltage (of the type measurable with a standard voltmeter) and electromotive force are not equivalent, but voltage results from electromotive force combined with a mechanism for electrons to bunch up and produce electrical pressure. Typically, electromotive force and voltage exist together, with one volt of electromotive force resulting in one volt of electrical pressure. When current flows through a resistance—where Ohm's law is typically applied—there will be a measurable electrical pressure differential (voltage) across that resistance. Therefore, V may be more appropriate than E when expressing Ohm's Law, although E is more widely accepted.
In physics, electromotive force is represented by an italic, lower-case Greek letter epsilon (ε), with the Roman letter V reserved for voltage of the type measurable with a standard voltmeter. In electrical engineering, the Roman letter E is used to represent electromotive force mostly because other non-Roman symbols are rarely needed in relevant publications. It's troublesome enough to find an ancillary Greek letter with modern publishing techniques. One hundred years ago, it required finding a metal letter stamp (called a sort) of the right character from a different type tray for each usage of the symbol. Typewriters had no way to use Greek letters. Somewhere along the line, engineers just said, "To heck with it," and switched to the Roman letter E.
Ohm's Law and power sources
By definition, Ohm's Law cannot be applied directly to power sources.[3] For example, if you apply Ohm's Law to a battery—by dividing the battery voltage by the known inherent resistance of the battery—you will get a meaningless result. This goes likewise for the secondary of a transformer (covered under transformers in AC Circuits). You cannot apply Ohm's Law directly to the secondary of a transformer because, like a battery, it is the seat of electromotive force. To apply Ohm's Law to a power source, you must first apply any inherent resistance in series with the voltage. This discovery by Georg Ohm made it possible for him to develop his Law in the first place.This has caused confusion among novices and experts alike. Some, including people with advanced degrees in physics, attempt to apply Ohm's Law to lengths of wire that are the seat of electromotive force (due to the wires being embedded in varying magnetic fields). Mathematically applying the measured voltage between two points on said lenghts of wire to the known resistance between those points gives invalid results. They conclude that Ohm's Law (and Kirchhoff's Voltage Law, discussed later) fail under the specific conditions presented by the circuit in question. However, mathematically applying the resistance of said wire in series with the source electromotive force produces valid results.[4]
Ohm's contribution to science
If asked what contribution Georg Ohm made to science, virtually everyone will say he discovered Ohm's Law. However, more importantly and subtly, he discovered that a power source has embedded resistance and that this embedded resistance acts in series with the electromotive force produced by the power source. Without that discovery, he could not have discovered the law named after him. Ampère and others didn't understand this principle and thus failed to find the correct relationship between resistance and current. Today, the lack of knowledge of this principle is widespread, leading to multiple essays and videos explaining how Ohm's Law and Kirchhoff's Voltage Law fail in specific scenarios. However, if the resistance or impedance of the circuits in such scenarios is correctly applied in series with the sources of electromotive force, Ohm's Law and Kirchhoff's Voltage Law accurately predict the actions of the circuits. We will look at this more when we discuss Kirchhoff's Voltage Law.
Summary
The rules for Ohm's Law are:- If you know the voltage, divide the current or resistance into it to get the unknown value.
- If you don't know the voltage, multiply the resistance and current to get the voltage.
Exercises (hover your mouse over
the helicopter to see explanations):
-
You have a resistor that is marked as 5 ohms. You place a voltmeter
across the resistor and it reads 10 volts. How many amperes of current
are flowing through the resistor? ____________

-
A current meter in a circuit reads 0.1 ampere. You place a voltmeter across a resistor in the circuit and the meter reads 2.5 volts.
What is the resistance, in ohms, of the resistor?____________

-
A current meter in a circuit reads 2 amperes. A resistor in the
circuit is labeled as 10 ohms. What voltage will be read if a voltmeter is placed across the resistor?____________

-
A 500-ohm resistor is placed across the terminals of a 12-volt
battery. How much current do you expect to flow in the circuit?
____________

- Voltage is the product of current and resistance (E = IR).
- If you know any two of the following, voltage, current or resistance, you can calculate the third.
- If you know the voltage, divide into it.
- If you don't know the voltage, multiply.
Conductors, Resistors and Ohm's Law
—————————
| Vocademy |
