| Vocademy |
Decibels (dB)
You probably think that decibels are used to measure how loud sounds are. You are correct, but sound level is only one thing measured using decibels.
The decibel (dB) is a unit used to express power (energy transfer, not mathematical powers). Particularly, decibels are used to compare one power level to another, a power ratio. The decibel is based on logarithms (see above) and expresses relatively large ratios with small numbers. The decibel is based on a larger unit called the bel, named after Alexander Bell. One bel is a power ratio of 10:1, two bels is a ratio of 100:1, 3 bels is a ratio of 1,000:1, etc.
| One bel equals a ratio of 10:1 |
A decibel is one-tenth of a bel, so 10 dB is a ratio of 10:1, 20 dB is a ratio of 100:1 and 30 dB is a ratio of 1,000:1, etc.
|
10 dB
equals a ratio of 10:1 (10 dB = 1 bel) |
Decibels are always used to measure a power ratio. Some special forms of dB are used to measure absolute values (like dBm and dB SPL), but even these units actually measure a ratio. They compare one power level to a fixed reference level. Sometimes decibels are used to express voltage. However, this is only possible because there is a direct relationship between voltage and power. Here is the formula used to calculate a power ratio decibels:
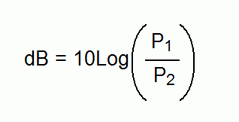 |
Where:
| dB | = | The power ratio in decibles |
| Log | = | The common logarithm |
| P1 | = | Power level 1 (output) |
| P2 | = | Power level 2 (input) |
Let's see how a
power ratio of 2:1 is expressed in decibels. For example, let's calculate the
gain in decibels for an amplifier that gives an output of 10 watts for an input
of 5 watts:
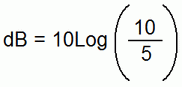 |
The steps to calculate this are:
- Divide the output power by the input power
- Find the logarithm of the quotient[1]
- Multiply the result by 10
Use the following key sequence on a calculator:
|
The answer is 3.0102999566398119521373889472449 decibels, which is nearly always shortened to 3 dB.
Voltage Expressed in Decibels
Decibels are only intended to express values of power. However, power and voltage are directly proportional to each other. Consequently, decibels can also be used to express voltage ratios. The formula to calculate decibels using voltage ratios is:
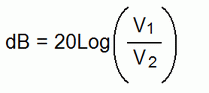 |
Be careful not to confuse decibels calculated from a voltage ratio with decibels calculated from a power ratio. More about this later.
Now that we have seen all the scary math, here is...
Everything You Need to Know About Decibels |
3 dB is a 2:1 ratio
10 dB is a 10:1 ratio
That's pretty much it. Three decibels is a two-to-one ratio and ten decibels is a ten-to-one ratio. You can extrapolate just about everything else from that. Let's carry this a bit further.
- 20 dB is a 100:1 ratio
- 30 dB is a 1,000:1 ratio
- 40 dB is a 10,000:1 ratio
Do you see a pattern here? For 10 dB (a ratio of 10:1) there is one zero in the ratio. For 20 dB (a ratio of 100:1) there are two zeros in the ratio, etc.
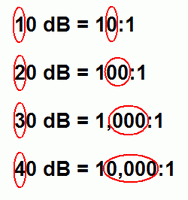 |
| The first digit in the dB expression is the number of zeros in the ratio. |
For example, if you see that a stereo amplifier has a channel separation of 60 dB, this means that the leakage of sound from one channel to the other is one-million-to-one (1,000,000:1). Notice that we have 60 dB and 6 zeros in the ratio.
A value of 60 dB is a ratio of 1,000,000:1
The power ratio represented by 60 dB has 6 zeros.
For another example, let's say an electronic instrument has a signal-to-noise ratio of 36 dB. What is that power ratio? Just by looking we can guess that 36 dB is about half-way between 30 dB and 40 dB. That's somewhere about half-way between 1,000:1 and 10,000:1; maybe somewhere around 5,000:1.
|
30 dB (1,000:1) 36 dB (≈ 5,000:1) 40
dB (10,000:1) |
| 36 dB is a power ratio somewhere between
1,000:1 and 10,000:1. Approximately 5,000:1 |
That's probably close enough. Now we know that when the signal we are measuring is at it's highest level it is about 5,000 times greater than the noise inherent in the instrument.
If we need to be more precise, we can narrow it down more than that. Let's start by figuring out what power ratio is represented by 33 dB. 30 dB represents a power ratio of 1,000:1. 3 dB represents a power ratio of 2:1. Let's put these together; you just add them:
30 dB + 3 dB = 33 dB
Easy enough. However, when we add decibels together we, are multiplying the ratios together. If you add 3 dB to another dB value, you are actually multiplying the other ratio by two. For example, 3 dB + 30 dB (33 dB) is the same as 2 x 1,000:1, which equals 2,000:1 (remember that 3 dB is a 2:1 ratio).
|
30 dB + 3 dB = 33 dB this is the same as 1,000:1 x 2:1 = 2,000:1 |
| When you add decibels you multiply power ratios. |
This shows us that 30 dB is 1,000:1 and 33 dB is 2,000:1. Now let's take that a step further by adding in another 3 dB
|
33 dB + 3 dB = 36 dB this is the same as 2,000:1 x 2:1 = 4,000:1 |
This shows that 36 dB is a 4,000:1 ratio. This is simply 30 dB + 3 + 3, which equals 36 dB, and is the same as 1,000:1 x 2 x 2, which is 4,000:1. Let's take a look at the steps:
- Start with 30 dB (1,000:1)
- Add 3 dB, which multiplies by 2 (2:000:1)
- Add another 3 dB, which multiplies by 2 again (4,000:1)
The bottom line is that every time you add 3 dB, you are multiplying by 2 (and every time you add 10 dB you are multiplying by 10). You may be asking if adding 6 dB multiplies by 4. Yes, it does. Here's a list of decibel values and how much they multiply:
- Adding 3 dB multiplies by 2 (2:1)
- Adding 6 dB multiplies by 4 (4:1)
- Adding 9 dB multiplies by 8 (8:1)
- Adding 10 dB multiplies by 10 (10:1)
- Adding 12 dB multiplies by 16 (16:1)
- Adding 15 dB multiplies by 32 (32:1)
You don't need the scary math to deal with decibels. Just remember that every 3 dB is a ratio of 2:1 (multiplies or divides by 2) and every 10 dB is a ratio of 10:1 (multiplies or divides by 10). Let's take a quick quiz:
| 1. | The output of an amplifier has twice the power of the input. What is the gain in dB? |
| 2. | The output power of a fiber optic cable is half of the input power. What is the loss in dB? |
| 3. | The output power of an RF amplifier is 200% of the input power. What is the gain in dB? |
| 4. | An attenuator has an output power of 50% of the input power. What is the loss in dB? |
| 5. | An antenna concentrates the power applied to it in such a way that a 500-watt input acts as if it were 1,000 watts. What is the gain of the antenna in dB? |
| 6. | An audio preamplifier provides a 2-watt output with a 1-watt input. What is the gain of the amplifier in dB? |
The answer to every question is 3 dB. In each case, there is a 2:1 ratio,
which is 3 dB. A loss is expressed as negative decibels, so a 2:1 loss is
What About 0 dB, 1 dB and 2 dB
0 dB is not the absence of power. If you find that a circuit has a gain of 0 dB, this means that the output power is the same as the input power; 0 dB means no gain or loss, a ratio of 1:1. If your circuit has 10 watts in and 10 watts out, you have a gain of 0 dB. 1 dB is a power ratio of 1.26:1 and 2 dB is a power ratio of 1.6:1.
| 0
dB = 1:1 1 dB = 1.26:1 2 dB = 1.6:1 3 dB = 2:1 |
The ratios represented by 3 dB and below
More on Decibels and Voltage
Now we need to make a quick return to voltage expressed in decibels. Recall the formula to calculate power:
P = EI
Power is current multiplied by voltage. Therefore, if you double the voltage you double the power, right? WRONG!
When you double the voltage, you don't double the power.
Don't forget your basic Ohm's Law. The current is dependent on the voltage. If you double the voltage, you will double the current. Let's see an example of how that affects the power.
10 V x 10 A = 100 W
Now let's double our voltage. Doubling the voltage also doubles the current, so we get the following result:
20 V x 20 A = 400 W
Doubling the voltage quadrupled the power.
Doubling the voltage of a circuit quadruples the power.
A 2:1 voltage ratio creates a 4:1 power ratio, which is 6 dB. Be careful when expressing a voltage ratio in decibels. A 2:1 power ratio is 3 dB, but a 2:1 voltage ratio is 6 dB.
A 2:1 voltage ratio is 6 dB, not 3 dB.
When expressing a voltage ratio in dB, remember to multiply the dB value by two compared to expressing power as dB. Expressing voltage ratios in dB only works in linear circuits. In non-linear circuits—where doubling the voltage more than doubles the current—do not express voltage in decibels.
The Level of Three-Decibels is Special
The quantity of 3 dB appears often. For example, the power level of a sound must double before a typical human can hear any increase in the loudness (you must double the power to hear any increase in volume). That's a 3 dB change[2]. For you to see a change in the brightness of a light, the power level must increase by a 3 dB (for you to see the light get brighter, its power must double).
The official range of human hearing is from 20 Hz to 20 kHz. This means that our ears become less and less sensitive to sounds as the frequency goes below 20 Hz. The frequency of 20 Hz is the point where we just start to hear a drop in loudness. This means that at 20 Hz our ears are half as sensitive as at higher frequencies. This is where the sensitivity of our ears drops by 3 dB. The same thing happens at higher frequencies. Our ear sensitivity drops by 3 dB at 20 kHz and our ears are less and less sensitive as frequencies go above that. Therefore, the range of human hearing is the range of frequencies between the points where our sensitivity drops by 3 dB.
The range of human vision is determined by the wavelengths (or frequencies) where our eyes become less sensitive by 3 dB. Therefore, the beginning of infrared—light with wavelengths too long for us to see—officially begins at 700 nm, where our eyes are half as sensitive than at shorter wavelengths. Ultraviolet begins at 400 nm, where our eyes are half as sensitive than they are to longer wavelengths.
We measure the frequency response range of an amplifier by where its response drops by 3 dB. Let's say an amplifier has an output of 100 watts at a frequency of 1,000 Hz. While testing the output over a range of frequencies, you find that the output drops to 50 watts at 100 Hz (with no change in the input power). This is the low-frequency half-power point; the output is 3 dB below the peak. Testing at higher frequencies you find that the output power drops to 50 watts at 10,000 Hz. The range of frequencies between these lower and upper half-power points (also called the cut-off frequencies) is the frequency range of this amplifier. The amplifier has a frequency response from 100 Hz to 10,000 Hz.
Absolute Decibels
Now that we have seen how decibels are used to express power ratios, let's see how they are used to express absolute power levels. We have seen that 3 dB is a 2:1 ratio, whether that is 1 watt to 2 watts or 1,000 watts to 2,000 watts. However, we can use dB to express an absolute value of watts if the ratio is compared to a fixed value.
dBm and dBu
One measure of absolute power is dBm. To express a value in dBm, we use a fixed reference of 1 mW. For example, how do you express 2 mW as decibels? You can't. Decibels always express a ratio of watts. However, how does 2 mW compare to 1 mW? It's simple: 2 mW is twice the value of 1 mW; it's a 2:1 ratio. Recall that a ratio of 2:1 is expressed as 3 dB. Therefore, 2 mW is 3 dB greater than 1 mW. Let's put a little m next to that to tell everyone that we are using 1 mW as our reference.
|
3 dBm |
| The m after dB means we are comparing to a fixed value of 1 mW |
Now, anyone in the know can see that our 2:1 ratio is compared to 1 mW. Knowing this we know this means we are expressing a value that is 3 dB greater than 1 mW (1 mW multiplied by 2), so it represents 2 mW
3 dBm = 2 mW
How do you express 10 mW in dBm? 10 mW is 10 times 1 mW. That's a 10:1 ratio, so 10 mW is 10 dBm.
10 dBm = 10 mW
How about 1 mW? This can be a bit confusing so follow carefully. What is the ratio of 1 mW compared to 1 mW? It's a 1:1 ratio. A 1:1 ratio is 0 dB (no difference). Therefore, 1 mW is represented by 0 dBm. Be careful. 0 dBm is not an absence of power. 0 dBm represents a power that has no difference from 1 mW. Therefore, 0 dBm is 1 mW.
0 dBm = 1 mW
Here's a chart of absolute power levels expressed in dBm.
| Absolute Power | dBm |
| 1 mW | 0 dBm |
| 2 mW | 3 dBm |
| 10 mW | 10 dBm |
| 100 mW | 20 dBm |
| 1 W (1,000 mW) | 30 dBm |
As shown above, 1 watt compared to 1 mW is a 1,000:1 ratio, so 1 watt is 30 dBm.
How about power levels less than 1 mW? When we have a loss, we express that as negative dB values. Therefore, power levels below 1 mW are negative dBm values. For example, 0.5 mW is one-half of a milliwatt. This is a 2:1 ratio compared to 1 mW and is expressed as -3 dBm.
-3 dBm = 0.5 mW
Consequently, 0.1 mW is a 10: ratio below 1 mW. This is expressed as -10 dBm. Here is the same chart as above with some levels below 1 mW added:
| Absolute Power | dBm |
| 0.001 mW | -30 dBm |
| 0.01 mW | -20 dBm |
| 0.1 mW | -10 dBm |
| 0.5 mW | -3 dBm |
| 1 mW | 0 dBm |
| 2 mW | 3 dBm |
| 10 mW | 10 dBm |
| 100 mW | 20 dBm |
| 1,000 mW (1 W) | 30 dBm |
Do Negative dBm Values Represent Negative Power
Don't be confused by power levels expressed as negative dBm values. This does not represent negative power; no such thing exists. A negative dBm value represents a power level that is less than 1 mW.
Why Use dBm Instead of Watts
Measuring power levels in dBm has some advantages. One is that a wide range of values can be expressed with small numbers. The other is that when you subtract a lower dBm value from a higher one, the result is a value in dB (dBm is an absolute value, but dB is a ratio).
Measuring Gain or Loss
A quick reminder before we tackle this:
- 1 mW = 0 dBm
- 2 mW = 3 dBm
-
When we double the power we see a 3 dB increase. Therefore:
- 4 mW = 6 dBm
- 8 mW = 9 dBm, etc.
- 10 mW = 10 dBm
For example, let's measure the gain of a preamplifier in dB. The obvious way to do this is to measure the input power and subtract that from the output power. Let's say you have an input power of 4 mW and an output power of 14 mW. That's a gain of 10 mW or 3.5 times. Now divide 14 by 4, find the logarithm of the quotient then multiply that by 10. That's a gain of 5.4 dB (rounded).
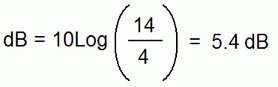 |
Calculating the gain of a preamplifier in dB starting with measurements in mW. |
Let's do that again, but this time using a power meter that represents power in dBm rather than milliwatts.
4 mW is 6 dBm and 14 mW is 11.4 dBm. This makes the input power 6 dBm and the output power 11.4 dBm. Subtract 6 from 11.4 and the answer is 5.4.
| 11.4 dBm - 6 dBm = 5.4 dB |
Calculating the gain of a preamplifier in dB, starting with measurements in dBm. |
This shows that if you subtract one dBm level from another, the result is a quantity in dB. This is easier than calculating the gain in decibels starting with a difference in watts? Let's double the input power and see if that works again. Now we have 8 mW in and 28 milliwatts out. Again, a gain of 3.5 times. Do the math and we get 5.4 dB again, just as we should.
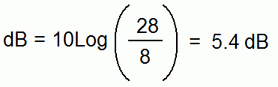 |
Calculating the gain of a preamplifier after doubling the input power |
Let's start by measuring in dBm and try again. That's an input of 9 dBm and an output of 14.4 dBm (notice that doubling the power added 3 dB to each number). Again, we get 5.4 dB.
| 14.4 dBm - 9 dBm = 5.4 dB |
Calculating the gain of a preamplifier after doubling the input power from 6 dBm to 9 dBm. |
When we want to measure gain or loss, we often use instruments that represent power in dBm rather than watts. Then all we have to do is subtract the smaller number from the larger number to get the gain or loss in dB.
When you subtract one level measured in dBm from another, the answer is a level in dB.
What about dBu?
DBu is essentially the same as dBm. Technically, it's the RMS voltage that results in 1 mW in a 600-ohm resistor, which is 0.775 VRMS. This comes from the standard impedance of a telephone circuit, which is 600 ohms. Audio systems tend not to match output impedance to input impedance between components because they are not trying to maximize power transfer but seek to maximize voltage while minimizing current. Therefore, the output impedance of a component will be around 600 ohms, whereas the input impedance will be around 10,000 ohms. This complicates the relationship to dBu, but audio engineers tend to "hand wave" this, seeing that they are not designing and building equipment; they are just making it work. What does an audio engineer need to know about dBm vs dBu? Keep the needles out of the red.
Sound Level
When you hear the term decibels or dB, the first thing you probably think of is "sound level". This is because a particular variety of absolute power level is used to express sound levels. This gives the erroneous impression that dB is an absolute measurement by itself.
SIL, dB SPL and dBA
The loudness of sound is measured in a unit called dB SPL (sound pressure level), often called SIL (sound intensity level) and is referenced to 20 micropascals, which is the approximate threshold of human hearing[3]. Therefore a sound level of 3 dB SPL is twice the power level of the threshold of human hearing. 60 dB SPL is 1,000,000 times the threshold of human hearing. The threshold of pain is about 120 dB SPL or 1,000,000,000,000 times the threshold of hearing.[4]
The term dB SPL is commonly accepted by electrical engineers. Audio technicians use the term SIL. The accepted notation for formal scientific writing is Lp/(20 μPa).
dBA refers to sound pressure measurements where a filter is used to emphasize frequencies in the 3-6 kHz range, where the human ear is most sensitive.
Antenna Gain
All radio transmitting antennas concentrate their radiated power in various directions. This means that if you are in the direction that the power is concentrated, you will receive a stronger signal than if the antenna radiated its power equally in all directions. This phenomenon is called antenna gain. Some antennas are called directional antennas because they are designed to concentrate their power in a specific direction and to a greater concentration than simpler antennas. Antenna gain is specified in dBi or dBd depending on the reference gain.
dBi
dBi is used to specify antenna gain where the reference is a theoretical antenna called an isotropic radiator. An isotropic radiator would radiate energy equally in all directions. Let's say an antenna concentrates power in one direction such that the power is twice as dense in that direction as it would be from an isotropic radiator. That antenna has a gain of 3 dBi.
dBd
dBd uses a half-wave dipole antenna as its reference. A half-wave dipole concentrates power along a plane perpendicular to the length of the antenna. This concentrating of power gives the half-wave dipole antenna a gain of 2.15 dBi. Therefore, an antenna with a gain of 1 dBd has a gain of 3.15 dBi. Since a half-wave dipole is a practical antenna and an isotropic radiator is a theoretical antenna, some people believe dBd is a more practical measurement.
A Quick Look at Decibels
| Vocademy |