| Vocademy |
Scary Math Review
Logarithms
In electronics, we often have to deal with huge numbers and tiny numbers. For example, we sometimes work with millionths of amperes (microamps). Other times we work with radio frequencies in the millions of billions of cycles per second (megahertz or gigahertz). When working with such numbers, we use scientific notation as discussed earlier. When it comes to power, we may deal with amplifiers that turn microwatts into megawatts. This is a range of 12 orders of magnitude (one order of magnitude means to multiply by 10). When working with such wide ranges of values, there is another tool to make things manageable. This tool is the decibel (dB). Before we can talk about decibels, we need a cursory understanding of logarithms. Logarithms are based on numeric powers, so let's talk about them first.
Powers
Power
is expressed by writing a number in superscript to the right of another
number. The number in superscript tells how many times to multiply the other
number by itself. Here is an example:
6
2
Six
squared or six to the power of two
The number 2 in superscript means to multiply the number 6 by itself,
which is 6 x 6 (notice the two sixes).
|
||||||
|
|
This is called squaring the number (it calculates the area of a square). You would say "six squared" or "six to the power of two." It is also sometimes called raising a number to a power. In this case, we are raising six to the power of two. The result is 36. The number that is being raised to a power is called the base. In this example, we have the base of six raised to the power of two. Now let's raise six to the power of three:
|
||||||
|
|
This is called cubing the number (it calculates the volume of a cube). This tells you to multiply six by itself, then multiply six by itself again. This would be 6 x 6 x 6, which is 216. Now let's raise six to the power of ten:
|
|||
|
|
This would be 6 X 6 X 6 X 6 X 6 X 6 X 6 X 6 X 6 X 6 or 60,466,176.
Multiplying Powers
To multiply two numbers of the same base to different powers, simply add the powers. For example:
| 6 | 2 | x | 6 | 3 |
is the same as
| 6 x 6 times 6 x 6 x 6 |
which is also the same as
| 6 x 6 x 6 x 6 x 6 |
which is also the same as
|
In each case, the result is 7,776. This only works if the base numbers are the same. This would not work for something like 43 x 75. If you have different bases you must calculate the powers first (the order of operations is Powers, Exponents, Multiplication, Division, Addition then Subtraction [PEMDAS]).
Logarithms
We can express that as an algebraic formula:
|
|||
|
|
Now that we see how to express powers as an algebraic formula let's learn some new terminology. The power that the base is raised to, the superscript
x, is also called the logarithm. Particularly, it is the logarithm of y to the base of b.| BaseLogarithm = Answer |
|
|
This means that 610 = 60,466 means that 10 is the base-6 logarithm of 60,466,176. Not too difficult, is it? Six isn't used as the base of a logarithm very often, let's use a more common logarithm. In fact, make that the common logarithm, the base 10 logarithm. Here it is expressed in the algebraic formula as above:
|
|||
|
|
Let's take another look at 10 squared (10 to the power of 2), just to get a feel for it before we move on:
|
|||
|
|
Now let's express that using the common logarithm:
| Log(100) = 2 |
|
|
Yikes! That looks more confusing than useful. It will become useful a bit later. For now, we'll do the same thing with 10 cubed and 10 to the fourth power:
| 103 = 1,000 |
|
is the same as |
| Log(1,000) = 3 |
|
Ten cubed and the logarithm of 1,000 |
| 104 = 10,000 |
|
is the same as |
| Log(10,000) = 4 |
|
Ten to the fourth power and the logarithm of 10,000 |
Do you see a pattern emerging? Notice that the logarithm equals the number of decimal places after the first digit (in these simple examples, the number of zeros).
Now let's take a quick look at how we can use logarithms to simplify multiplication. Here's an example of multiplication as we know it:
|
100 X 1,000 = 100,000 Multiplication as you know it |
We can do that using logarithms. Here are the steps:
- Get the logarithm of the first number
- Get the logarithm of the second number
- Add the logarithms
- Get the antilogarithm (the reverse of the logarithm) of the sum
Let's do the multiplication. You can use a calculator, slide rule or log tables in the back of an old math book to follow along:
| Formulas |
Calculator (Your calculator may use memory differently) |
Steps | |||||||||||
Log(100) = 2 |
|
Find the logarithm of 100 and store it in memory | |||||||||||
| Log(1,000) = 3 |
|
Find the logarithm of 1000 | |||||||||||
| 2 + 3 = 5 |
|
Add the two logarithms (recall the first from memory) | |||||||||||
| Antilog(5) = 100,000 |
|
Find the common antilogarithm of the answer |
The antilogarithm of 5 (105) is 100,000. Therefore:
100 X 1,000 = 100,000
Wasn't that easy? Well, it's easy for computers. That's one place where logarithms are used for multiplication. You can also make machine parts with curves based on logarithms. By doing that we can make machines move shafts or levers based on multiplying one movement by another. This technique reached its apex with analog fire control computers used aboard ships. These mechanical monsters calculated the firing angles and powder charges for shipboard guns before the development of digital computers. A squad of sailors turned cranks and dials to give the inputs for the ship's speed, course, wind, target speed, target course, etc. Using these computers made it possible for a moving ship to hit another moving ship at a distance. Ships were able to score hits often enough that they no longer had to battle it out yardarm-to-yardarm in hopes of hitting something. (See the video at the end of this page if you want to see how these analog computers worked.)
Logarithms and graphs
One of the most common uses of logarithms is in graphing. For example, the human ear responds to frequencies from 20 cycles per second to 20,000 cycles per second (20Hz to 20kHz). This is a considerably wide range. Also, the ear does not respond evenly. When the frequency is doubled, then doubled again, we hear what sounds like even intervals. For example, a frequency of 55Hz is a musical A, so is 110Hz, 220Hz, 440Hz, 880Hz, 1,760Hz and so on up to the highest A we can hear, which is 14,080Hz. If you try to draw a graph of these frequencies you will find that the lower frequencies are close together and the higher frequencies further apart. It becomes impractical to show such a wide range on a single graph.
 |
| A frequency domain graph of several octaves of the musical A plotted on a linear scale. Each A is double the frequency of the next lower A. However, it sounds like even intervals to us. |
As you can see, the graph runs out of room quickly as the intervals double. This graph has only five octaves. To draw this graph and include the A at 14,080 Hz, the graph needs to be about twice as wide as above. If you shrink it to a more manageable size, the lower frequencies are squeezed too close together.
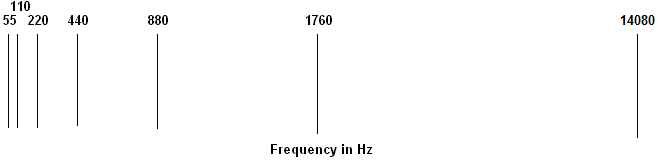 |
| Here we have added the next-higher octave and squeezed the graph into the same space. It's getting a bit crowded in the lower frequencies. |
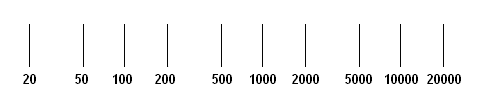
The following is a logarithmic scale:
 |
| A logarithmic scale. |
If you take a close look at this scale, you will see that the distance between 1 and 10 is the same as the distance between 10 and 100. Likewise, you will see that the distance between any number and double that number is the same as the distance between 1 and 2. For example, the distance between 2 and 4 is the same as the distance between 4 and 8, or between 30 and 60. This continues in either direction.
There is no 0 on a logarithmic scale. The numbers just get smaller and smaller
as you go to the left. Each time you go the distance between 1 and 10 to the
left, you just get a number 10 times smaller than the one before. Likewise, each
time you go the distance between 1 and 10 to the right, you get a number 10
times larger than the one before.
The following is a logarithmic scale
that spans from 20 to 20,000. This can be used as a scale to plot the range of
human hearing (from 20Hz to 20kHz).
 |
| A logarithmic scale of the numbers from 20 to 20,000. |
Notice that this scale can squeeze a large range into a convenient, smaller size.
 |
| https://xkcd.com/1162 |
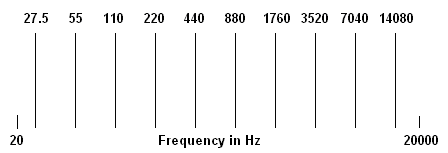
Using this scale, we can make a frequency domain graph of the frequencies that musicians call an "A". Now these frequencies fit into a conveniently-sized graph. Notice that the distance between each pair of As is spaced evenly. Another consequence of plotting the frequencies on a logarithmic scale is that the frequency of 1,000 Hz (1 kHz) lands near the middle of the graph, which is right about where we perceive it. This is why 1 kHz is the standard frequency for testing audio circuits.
 |
|
This is a frequency domain graph of the musical A plotted on a logarithmic scale. Now the octaves are evenly spaced, just as we perceive them. |
A typical healthy person can perceive a difference in loudness when the sound pressure changes by a factor of 2[2]. In other words, if the loudness of a sound increases, the sound pressure has to double before most people can tell that a sound got louder. For a sound to seem twice as loud, the sound pressure has to increase by a factor of 10. The range of loudness that we can hear also covers an extensive range. The loudness of a sound that a typical person can barely hear is called the threshold of hearing. The loudness of a sound so loud that it is painful is called the threshold of pain. A sound at the threshold of pain exerts about 1,000,000,000,000 times as much pressure as a sound at the threshold of hearing. This is another range that is difficult to manage numerically. However, the logarithm of 1,000,000,000,000 is 120, a more manageable number.
If you make a graph of a range of frequencies against the loudness, you will normally use a logarithmic scale for both axes. The following scale is a two-dimensional scale that is logarithmic on both axes.
 |
| A scale that is logarithmic on both axes |
Plotting the sensitivity of the human ear on such a scale has the convenience of
reducing the range to a manageable size. Since wide ranges are common in
electronics, logarithms and logarithmic scales are commonly used.
The
following graph is the ideal frequency response of an audio amplifier. Using
logarithmic scales, the wide frequency response is shrunk to a manageable
size.
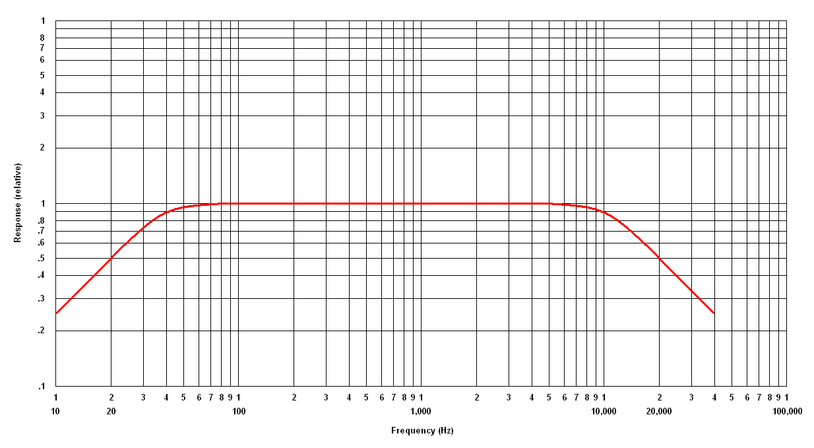 |
| The ideal frequency response of an audio amplifier. |
Notice that the amplifier responds equally (a flat response) to all frequencies between approximately 80 Hz and 5 kHz. At 20 Hz and 20 kHz the response is 50% of the maximum. These are called the half-power points. The typical human will notice a difference at these points. The frequency response of the amplifier is the range of frequencies between the half-power points. Therefore, this amplifier has a frequency response of 20 Hz to 20 kHz. In the above graph, the response drops off rather gradually at 50% per octave (doubling the frequency or cutting the frequency in half constitutes an octave). Using a logarithmic scale for both axes, this drop-off curve forms a straight line with a 40-degree angle.
Now that we have learned a little about logarithms let's go on to the next page and learn about decibels.
The following video is optional viewing. Among other things, it shows how machine parts can be made to shapes based on logarithms. Such shapes were used to perform mathematical calculations in mechanical computers.
Exponents and Logarithms
A video produced in 1977 by IBM illustrating the powers of ten.
The Powers of Ten
A video about the mechanical analog fire control computers used aboard ships during world war II.
Fire Control Computers (optional)
| Vocademy |