| Vocademy |
Summing Amplifier (mixer)
A summing amplifier is an inverting amplifier with multiple-inputs.
Each input connects to the inverting input of the op-amp through its own
resistor. The
input resistors are of equal value. The following examples use a feedback
resistor the has the same value as the input resistors. This will give the
summing amplifier a gain of 1 (actually a gain of
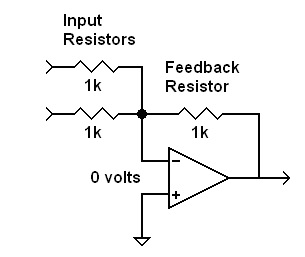 |
| Op-Amp summing amplifier |
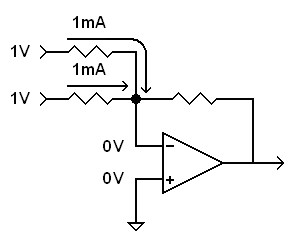
Recall that with the inverting amplifier, the non-inverting input of the op-amp is connected to ground (0 volts). The op-amp will adjust its output to whatever voltage it takes to keep the inverting input also at 0 volts. This makes the inverting input a virtual ground (see Inverting Amplifier). Each input resistor has one end tied to the virtual ground (0 volts) and the other end tied to an input voltage.
Let's put +1 volt on
each input. Each input resistor now has +1 volt on the input side and 0 volts at
the virtual ground side. Each resistor has a value of
 |
|
The current from the two inputs flows into the virtual ground. |
Where does this current go from there? There are two current paths from the inputs to the virtual ground. This is a parallel circuit (see DC Circuits,, Part 4). It may look like there are two current paths exiting the virtual ground. However, there is only one current path. Current cannot flow into the op-amp's inverting input because the impedance is too high[1]. That leaves only one path. That is through the feedback resistor to the op-amp's output. At the virtual ground, the feedback circuit becomes a series circuit. Following Kirchhoff's Current Law, 2 mA of current leave the virtual ground and flow through the feedback resistor and into the op-amp's output (the output is sinking current, see sourcing and sinking current).
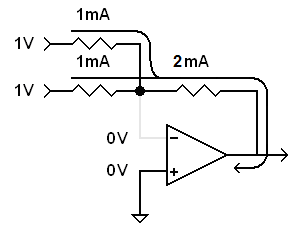 |
| The two 1 mA currents combine into a 2 mA current that flows through the feedback resistor and into the op-amp's output. |
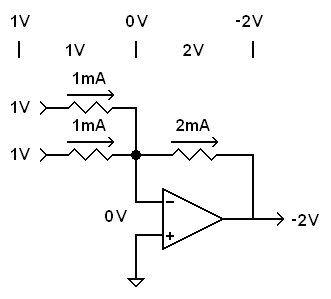
Recall that each of the three resistors has a value of 1 k. Each input resistor has 1 volt across it and therefore 1 mA of current flowing through it. The feedback resistor has 2 mA of current flowing through it, so it must have 2 volts across it.
 |
|
The circuit loses 2 volts from the virtual ground to the op-amp's output,
making the output voltage |
We start with 1 volt at
each input. We lose 1 volt across each input resistor as current flows to the virtual ground.
We then we lose 2
volts across the feedback resistor. This leaves us with
Don't forget
which is the cause and which is the effect. The voltages and currents we just
examined don't force the op-amp's output to
Now, let's put +1 volt at one input and +2 volts at the other. This may seem to make things more complicated, but it doesn't. Once the op-amp settles on an output voltage that makes the inverting input see 0 volts, we have 1 mA going through one input resistor and 2 mA going through the other. These currents combine into 3 mA going through the feedback resistor.
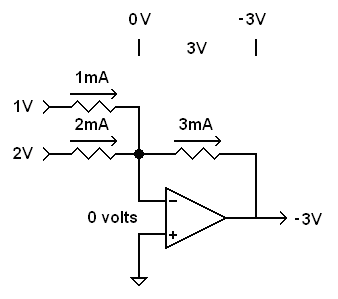 |
|
With the above input voltages, we end up with 1 mA and 2 mA combining into 3 mA through
the feedback resistor. This results in |
The 1 k feedback resister
now has 3 mA flowing through it, so it now has 3 volts across it. This results
in
Now let's really complicate things. Let's put a positive voltage on one input and a negative voltage on the other. Once the op-amp settles on a voltage that puts 0 volts at the inverting input, we have the following voltages and currents.
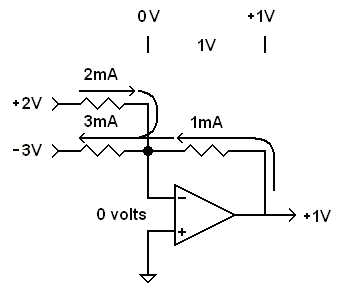 |
|
A summing amplifier with inputs of opposite polarity. |
The top resistor has +2 volts at the input and 0 volts at the virtual ground.
There must be 2 mA flowing through it into the virtual ground. The bottom resistor
has -3 volts at the input and 0 volts at the virtual ground. There must be 3 mA
flowing from the virtual ground, through the bottom resistor and out the bottom input.
Where do these three milliamps come from? 2 mA come from the top input, through
the virtual ground and right out the bottom input. The other milliamp must come
from the output of the op-amp and through the feedback resistor. The op-amp must
put +1 V on the output to make this happen. The sum of +2 and
If you need a summing amplifier that handles more inputs, you can just add more input resistors.
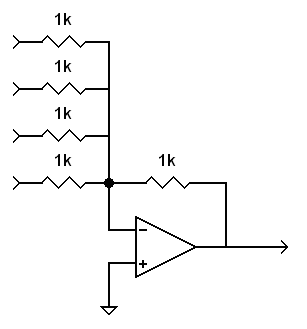 |
|
A four-channel summing amplifier. |
If you need the output to be the same polarity as the input, you can send the output of the summing amplifier to the input of an inverting amplifier.
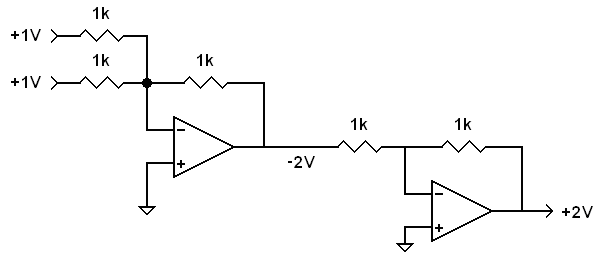 |
|
A summing amplifier with the output polarity the same as the input polarity. |
Operational Amplifiers No. 7 - Summing Amplifiers
Inverting and Summing Amplifiers - Answers to Questions
—————————
| 1 | A tiny current flows into the op-amp input, but it is so small that we can ignore it. |
| Vocademy |
