| Vocademy |
Converting Binary Numbers
Converting binary to decimal
Humans like to use decimal numbers, but we use binary numbers to represent what goes on in digital circuits. Because of this, it is often necessary to convert decimal numbers to binary and vice versa.
The following procedure will convert a binary number to its decimal equivalent. This example uses the binary number 10101101.
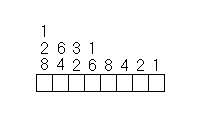 |
| First, create a table that looks like this. |
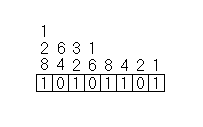 |
| Next, write the binary number in the table |
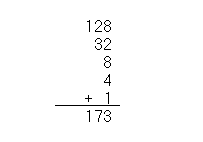 |
| Finally, add up the numbers that have a 1 below them. The sum is the decimal equivalent of the binary number. |
Therefore, 10101101 is 173 in decimal.
Converting Decimal to Binary
The following procedure converts a decimal number to its binary equivalent. This example uses the decimal number 182.
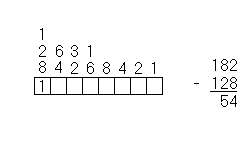 |
| Find the highest number that will divide into the decimal number you are converting and put a 1 in the cell below that number. In this case, 128 is the highest number that will divide into 182. Subtract this number from the original decimal number. |
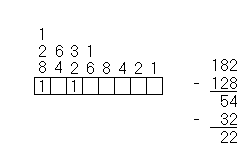 |
| Find the highest number that will divide into the remainder and put a 1 in the cell below that number. In this case, 32 is the highest number that will divide into 54. Subtract this number from the original remainder. |
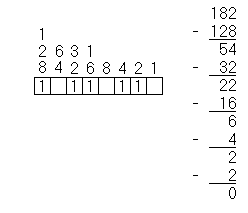 |
| Repeat this process until there is no remainder. |
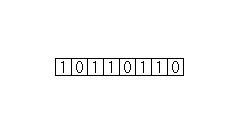 |
| Finally, fill in zeros between the ones. The binary number in the table is the binary equivalent of the original decimal number. |
Binary Addition
There are four rules for binary addition.
|
0 +0 0 |
| Rule 1, 0 + 0 = 0 |
|
0 +1 1 |
| Rule 2, 0 + 1 or 1 + 0 = 1 |
|
1 1 +1 0 |
| Rule 3, 1 + 1 = 0 and carry over to the next column to the left |
|
1 1 1 +1 1 |
| Rule 4, 1 + 1 + 1 (as with a carry from the column to the right) = 1 and a carry over to the next column to the left |
The following two 8 bit numbers, when added together, show all the binary addition rules in action.
|
1 1
1
0 0 1 1 0 0 1 1 + 0 0 1 1 1 0 1 0 0 1 1 0 1 1 0 1 |
| 1 + 1 + 1 (as with a carry from the column to the right) = 1 and a carry over to the next column to the left |
| Vocademy |
