| Vocademy |
Logic Gates
Most digital circuits consist of logic gates. A logic gate can be
made from diodes or transistor in different arrangements. However, when working
with logic gate, you do not need to know what is going on inside. All you need
to know is what output results from a particular input.
A logic gate
will have several inputs and (usually) one output. Each input will be able to
accept one of two possible voltages. For example, an input to a
transistor-transistor logic (TTL) circuit must be either +5 volts or 0 volts.1 A
CMOS logic circuit can operate with a supply voltage ranging from +3 volts to
+12 volts. The high input voltage depends on the supply voltage. If operated
from +12 volts than a particular input to the circuit will accept either 0 volts
or +12 volts. The point is that an input can accept either of two voltages. To
avoid ambiguity, the input voltages must be close to those that are expected by
the circuit.
To simplify the analysis of logic gates the high and low
voltages will be referred to as either 0 or 1. For example, with a TTL circuit,
a logical 0 is represented by 0 volts and a logical 1 is represented by +5
volts. Therefore, a logic gate can have several inputs. Each input will have
either a 1 or a 0 presented to it. The output of the gate will depend on the
design of the gate.
There are three basic logic gates. These are the OR
gate, the AND gate and the Inverter (sometimes called a NOT). All other gates
are derived by combining these three gates.
The OR gate
OR gate will have two or more inputs and one output. The following diagram represents a two input OR gate. Next to the diagram is a truth table. This tells what the output of the gate will be based on the inputs. These values are shown as logical 1s and 0s.
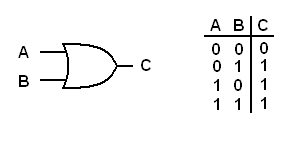 |
| The OR gate and its truth table |
The OR gate is used to detect the presence of a logical 1 at any of its inputs. The formal way to explain the OR gate is "if input A is a logical 1 or input B is a logical 1 then output C will be a logical 1." Therefore the output of an OR gate will be a logical 1 if any input is a logical 1.
The AND gate
Like the OR gate, the AND gate will two or more inputs and one output. The following diagram represents a two-input AND gate with its truth table.
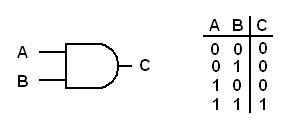 |
| The AND gate and its truth table |
The AND gate is used to detect the presence of logical 1s at all of its inputs. The formal way to explain an AND gate is "if input A is a logical 1 and input B is a logical 1 then output C will be a logical 1." Therefore the output of an AND gate will be a logical 1 if all inputs are logical 1s."
The inverter
The inverter has a single input and a single output. The following diagram represents an inverter.
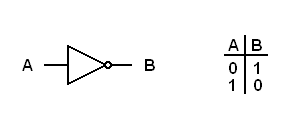 |
| The inverter and its truth table |
The inverter is used to change a logical 1 to a logical 0 and vice versa. The output of an inverter is opposite to the input.
All logical circuits are derived for these gates. Other gates will be discussed below, but all other gates are derived from the AND gate, the OR gate and the inverter. A modern microprocessor will have millions of transistors. With all its complexity, a computer is made of nothing more than AND gates, OR gates and inverters.
The Exclusive OR gate
Another basic gate is the Exclusive OR (XOR) gate. This gate has a basic useful function, but it is derived from a combination of OR gates, AND gates and inverters. The following diagram shows how the Exclusive OR function is obtained from the basic gates.
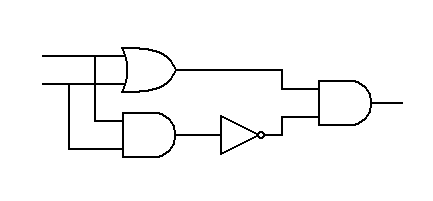 |
| The Exclusive OR function derived from the basic gates. |
This will create the Exclusive OR function. You can follow the gate operation in the exercise below. However, here is a more elegant version of an Exclusive OR gate.
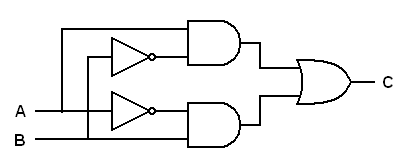 |
| Another Exclusive OR function derived from the basic gates. |
Both of the above sets of gates will perform the Exclusive OR function, as you
will see in the exercises below.
The following diagram represents the Exclusive OR gate with a truth table.
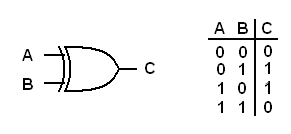 |
| The XOR (Exclusive OR) gate and its truth table. |
The Exclusive OR gate is used to detect a difference between its inputs. The formal way to explain an Exclusive OR gate is "if input A is a logical 1 OR input B is a logical 1 then output C will be a logical 1 unless both inputs A and B are a logical 1." Therefore the output of an Exclusive OR gate will be a logical 1 if the inputs are different."
Exercise:
Trace the logic
signals through the derived Exclusive OR gate.
In each of the following
diagrams, write the logical status (0 or 1) at each input to each gate. The
final result should match the Exclusive OR gate. Use the diagrams and truth
tables above for a reference. Remember: OR = output is 1 if any input is 1; AND
= output is 1 if all inputs are 1; XOR = output is 1 if the inputs are
different; Inverter = output is opposite to the input.
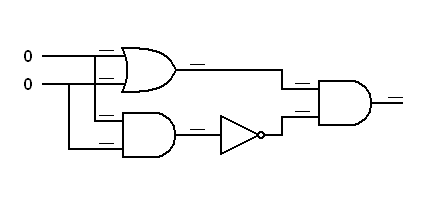 |

|
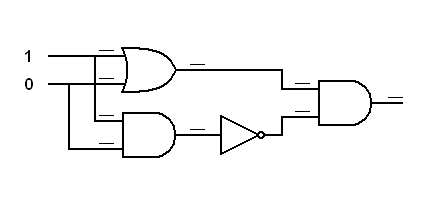
|
|
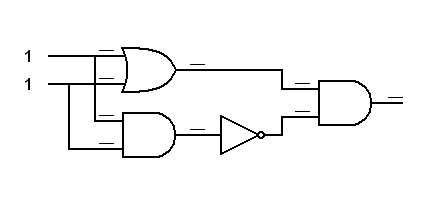
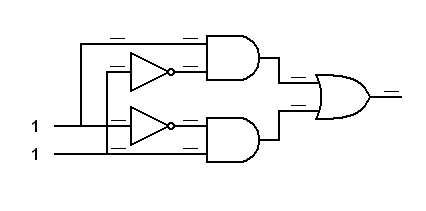
Here is the second version of the Exclusive OR gate. Trace the logic signals through it.
 |
|
|
|
The NOR gate
The NOR gate is derived from the functions of the OR gate and
the inverter. The following diagram shows an OR gate with an inverter on the
output and that the NOR gate has the same function.
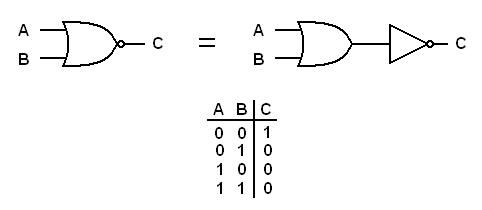 |
| The NOR gate, its equivalent gates, and truth table |
Rather than memorize a function for the NOR gate, remember that it works as an OR gate with an inverter.
The NAND gate
Similar to the NOR gate, the NAND gate is derived through the
functions of the AND gate and the inverter. The following diagram shows the NAND
gate and how it is derived.
 |
| The NAND gate, its equivalent gates and truth table |
The Exclusive NOR gate
As shown below, the Exclusive
NOR gate is derived similarly to the NOR and the NAND gate.
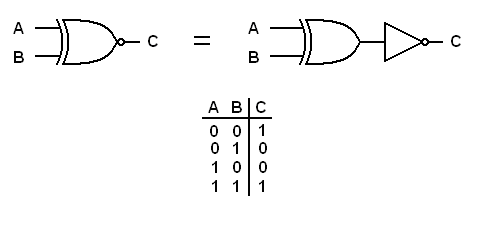 |
| The Exclusive NOR (XNOR) gate, its equivalent gates and truth table |
Other Derived Gates
Sometimes you
may need to create gates out of whatever you have available. For example, logic
gates come as integrated circuits. Often you may get more gates than you need.
These extra gates can sometimes be used to derive gates without adding more
integrated circuits. The following examples show how specific gates can be made
from other available gates. If anyone asks, these derived gates are described by
De Morgan's Theorems.
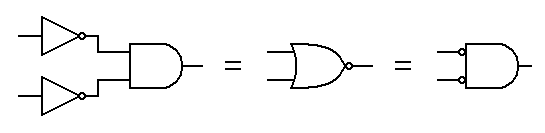 |
| NOR gate derived from inverters and an AND gate. |
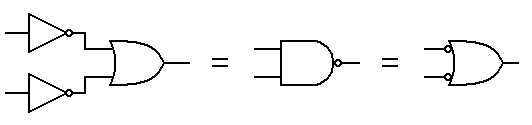 |
| NAND gate derived from inverters and an OR gate |
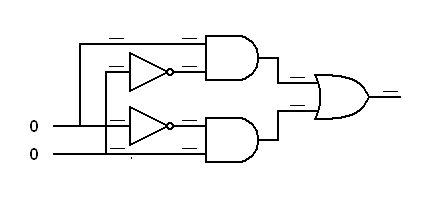
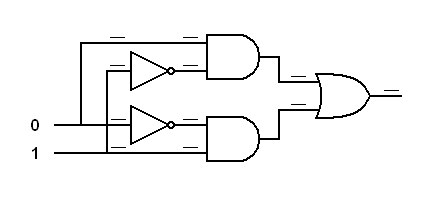
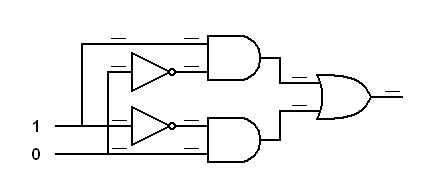
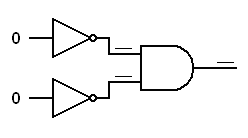
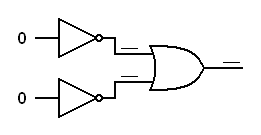
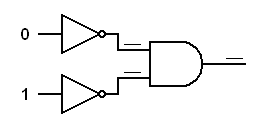
Exercise:
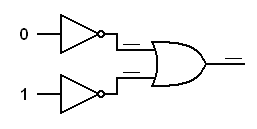
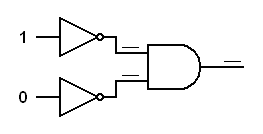
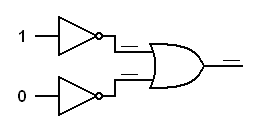
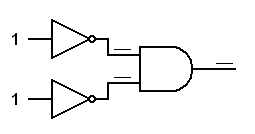
Trace the logic signals through the derived gates below.In each of the following diagrams, write the logical status (0 or 1) at each input to each gate. This will prove that an inverted input AND gate works like a NOR gate and an inverted input OR gate works like a NAND gate.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Answers to Exercises
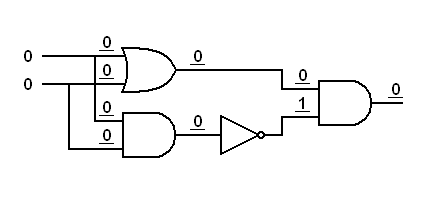 |
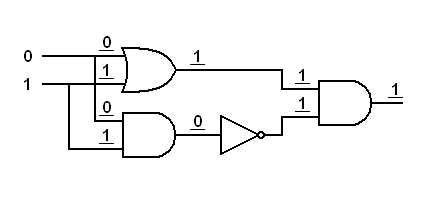
|
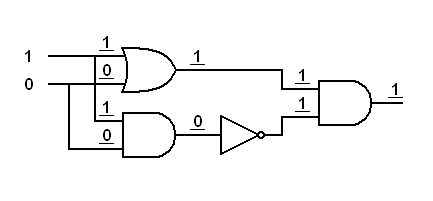
|
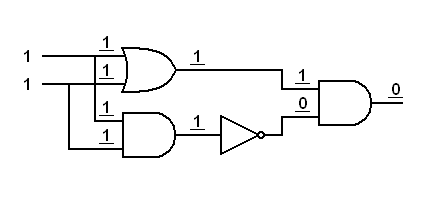
|
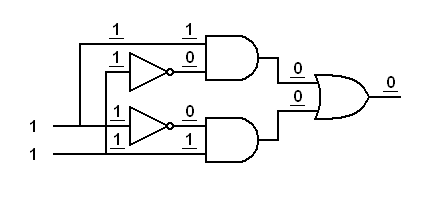
Here's the second version of the XOR gate.
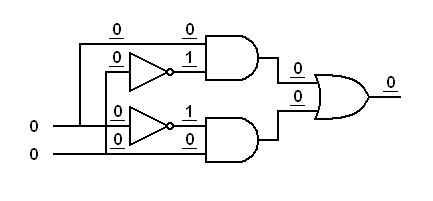 |
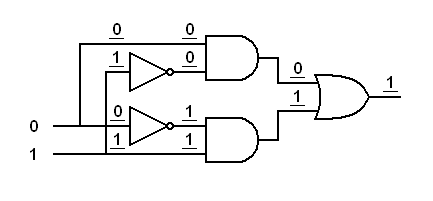
|
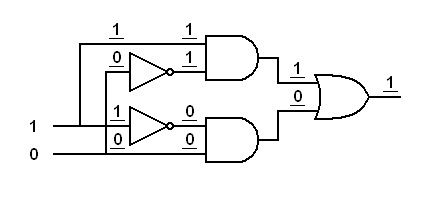
|
|
 |
1 |
 |
1 |
 |
0 |
 |
1 |
 |
0 |
 |
1 |
 |
0 |
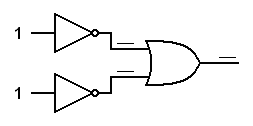 |
0 |
Review:
Move your mouse over the blank spaces to see the answers.
- Which gate
follows the description: The output is 1 if all inputs are 1?
- The AND gate.
- Which gate
follows the description: The output is 1 if the inputs have any difference?
- The Exclusive Or gate?
-
Which gate follows
the description: The output is 1 if any input is 1?
- The OR gate?
-
Which gate works
like an AND gate with an inverter on the output?
- The NAND gate?
-
With which gate is
the output opposite to the input?
- The Inverter or NOT?
-
If you put an inverter on the output of an Exclusive OR gate, what does it
become?
- An Exclusive NOR (XNOR) gate?
| Vocademy |