| Vocademy |
Digital to Analog Converters (DACs)
A digital to analog converter takes input from a digital circuit and converts it to a voltage that represents the digital value.| 8-bit Digital Input |  |
Output Voltage |
| A digital to analog converter | ||
For example, let's say you have a four-bit TTL counter. Each output wire will be either 5 volts or 0 volts depending on the state of the counter. There are 16 possible states and, as usual, 5 volts represents a logical 1 and 0 volts represents a logical zero. If these four outputs are placed on the input of a digital to analog converter, we will get something like the following voltages:
| Count | Output Voltage | Count | Output Voltage | |||||
| 0000 | 0 | 1000 | 8 | |||||
| 0001 | 1 | 1001 | 9 | |||||
| 0010 | 2 | 1010 | 10 | |||||
| 0011 | 3 | 1011 | 11 | |||||
| 0100 | 4 | 1100 | 12 | |||||
| 0101 | 5 | 1101 | 13 | |||||
| 0110 | 6 | 1110 | 14 | |||||
| 0111 | 7 | 1111 | 15 | |||||
In this example we have a very convenient one volt per count. For example, 0100, which is the decimal number 4 comes out to 4 volts. It isn't necessarily that way and probably isn't. The following table is also a valid conversion from digital to analog, and perhaps more realistic.
| Count | Output Voltage | Count | Output Voltage | |||||
| 0000 | 0.00 | 1000 | 0.40 | |||||
| 0001 | 0.05 | 1001 | 0.45 | |||||
| 0010 | 0.10 | 1010 | 0.50 | |||||
| 0011 | 0.15 | 1011 | 0.55 | |||||
| 0100 | 0.20 | 1100 | 0.60 | |||||
| 0101 | 0.25 | 1101 | 0.65 | |||||
| 0110 | 0.30 | 1110 | 0.70 | |||||
| 0111 | 0.35 | 1111 | 0.75 | |||||
As long as the output has equal steps in voltage for each count, the output is a valid analog representation of the digital input. Now we just need a circuit that will create this relationship.
A Simple Resistance Ladder DAC
The following circuit is a simple 4-bit digital to analog converter. It is a modified Op-Amp mixer where the input resistors are proportional to the bit weights of the input wires. The least significant bit goes to the 5k resistor. The next significant bit goes to the 2.5k resistor, which has half the resistance of the least significant bit. No matter how many inputs there are, each successive bit has half the resistance as the previous. The effect of this is that each successive bit, from least significant to most significant, contributes twice the current to the Op-Amp as the next lower bit.
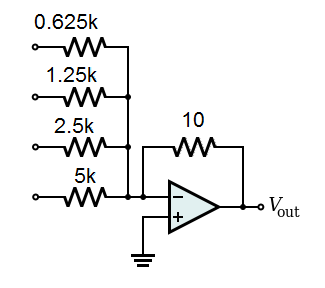 |
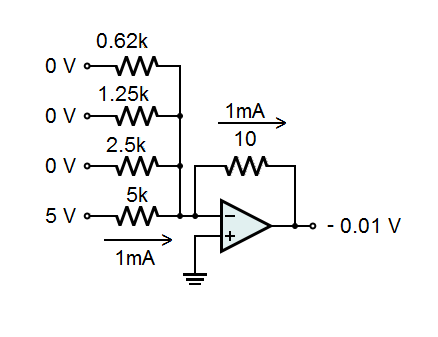
In the circuit below, the binary number 0001 is applied to the input. Using TTL voltage levels applies 5 volts to the 5k resistor and 0 volts to the other resistors. 1mA of current flows through the 5k resistor (5 volts divided by 5k = 1mA).
Recall that the Op-Amp will make it's output whatever it takes to make the two inputs equal. This means that with the non-inverting input grounded, as in this circuit, the inverting input will be held at 0 volts. Therefore, whatever voltage is applied to the left side of a resistor, that is the total voltage across the resistor. Also, remember that no current can flow into the inverting input. Therefore, whatever current goes through one of the input resistors, that current must combine with any other current from other input resistor and go through the feedback resistor to the Op-Amp output.
The 1mA that flows through the 5k resistor has nowhere to go but through the 10-ohm feedback resistor. The output to adjusts to -0.01 volts to compensate. Therefore, 0001 on the input results in -0.01 volts on the output.
 |
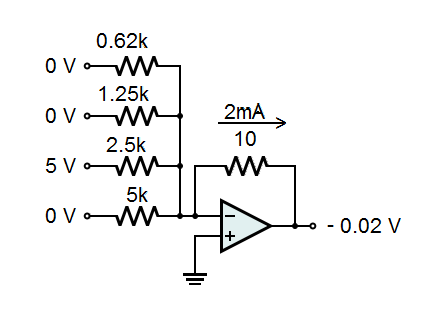
Now let's apply 0010 to the inputs. This applies 5 volts to the 2.5k resistor and 0 volts to the others. Now we get 2mA through the input resistor (5 volts / 2.5k). This 2mA flows through the feedback resistor, causing the Op-Amp to compensate with -0.02 volts on the output. Therefore, 0010 on the input results in -0.02 volts on the output. (The 2mA flowing through the 2.5k resistor is not shown to avoid clutter in the illustration.)
 |
Now let's apply 0011 to the inputs. Now we have 1mA flowing through the 5k resistor and 2mA flowing through the 2.5k resistor. Following Kirchhoff's current law, the two currents combine into 3mA through the feedback resistor. The output of the Op-Amp compensates by making the output voltage -0.03 volts.
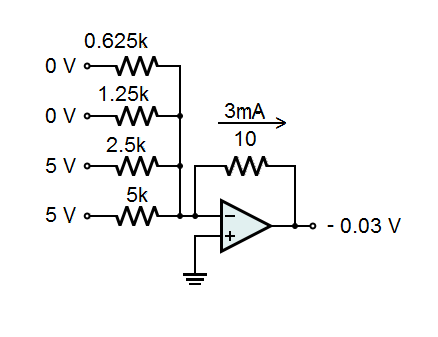 |
This continues through all 16 possibilities on the input, where 1111 results in an output of -0.15 volts.
R/R2 Ladder
The simple DAC is easy to understand, but it requires just the right resistors to make it work. The R/2R ladder version only requires two values of resistor.
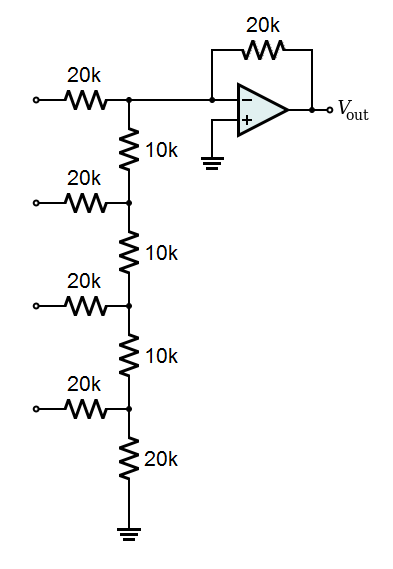 |
| A four-bit R/2R Ladder DAC with Op-Amp |
An engineer may be tempted to analyze the R/2R ladder using a combination of Thevenin's Theorem and Superposition Theorem, which is beyond the scope of this text. However, it can be analyzed using simple series-parallel circuit analysis, which you have already tackled (if not, you need to back up to Part 4, Lessons 1 and 2 in DC Circuits). To simplify it further, let's just use a two-bit input:
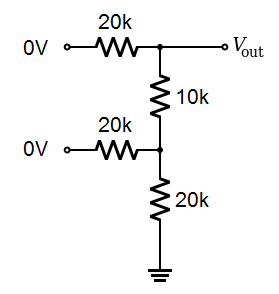 |
| A two-bit R/2R DAC |
In the above diagram, the input is a binary 00, both inputs are 0 volts. Here is the equivalent circuit. If you look carefully, you will see that it is the same circuit as above; the two inputs are shown as connected to ground (0V):
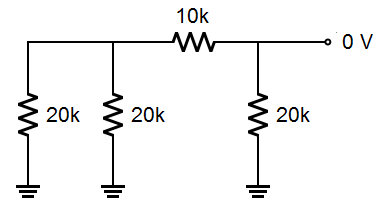 |
All the inputs are grounded, so there is no voltage anywhere in the circuit. The output is 0 volts. Now let's put a binary 01 on the inputs:
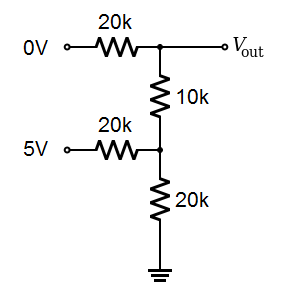 |
Here is the equivalent circuit for this state. Again, look carefully and you will see that it is the same circuit as above; the ground and input with 0V are shown connected to the negative terminal of the battery:
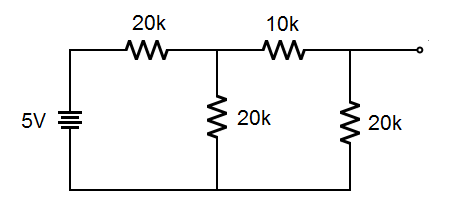 |
Now we can analyze the resistors as combinations of series and parallel connections as we learned to do in the basic DC circuits. Here is the breakdown of the circuit;
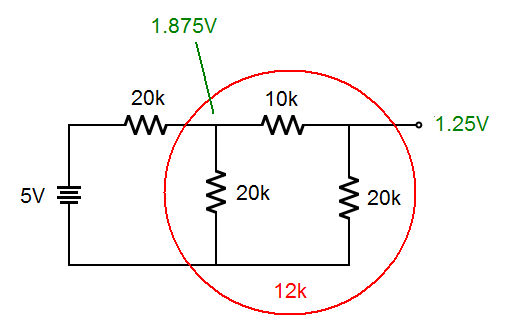 |
Notice that the right part of the circuit calculates out to be 12k in series with 20k. Following the rules for series circuits that gives us 1.875 volts at the indicated node. The voltage is divided proportionally between the circled and uncircled parts of the circuit. That puts 3.125 volts across the uncircled 20k resistor and 1.875 volts across the 12k presented by the circled resistors. This puts 1.875 volts across the last 10k and 20k resistors that are in series with each other. They act as a voltage divider where 1/3 of the voltage is across the 10k resistor, and 2/3 of the voltage is across the 20k resistor. This gives an output of 1.25 volts (2/3 of 1.875 volts).
Now lets put a digital 10 on the input.
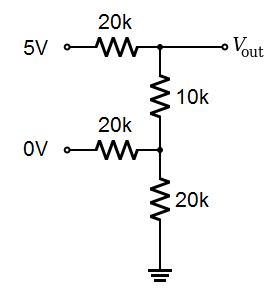 |
If the circuit is working, each step should increase the output voltage by equal amounts. Therefore, putting digital 10 on the input (going from decimal 1 to decimal 2) should give us 2.5 volts on the output. Let's see if that works. Here is the equivalent circuit:
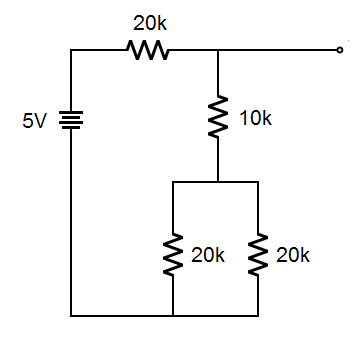 |
Look carefully again, and you will see that this is the same circuit as above. Now let's analyze it:
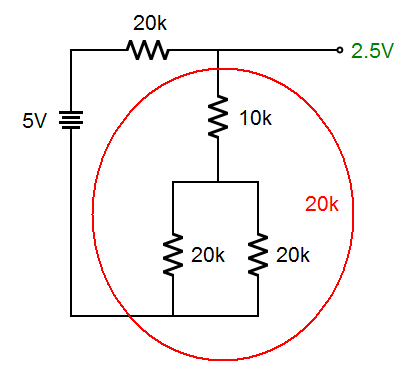 |
The three circled resistors act as a single 20k resistor in series with the uncircled 20k resistor. This makes a voltage divider with equal resistors, making the output voltage 1/2 of the battery voltage. The output is 2.5 volts. This is indeed an equal step from the 1.25 volts when the binary 01 (decimal 1) was on the input. Therefore the circuit did its job.
Now lets put a binary 11 (decimal 3) on the input and see if we get 3.75 volts out:
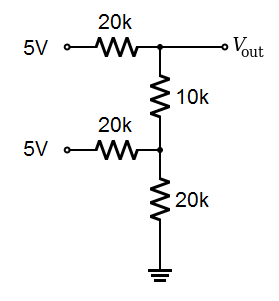 |
Here is the equivalent circuit:
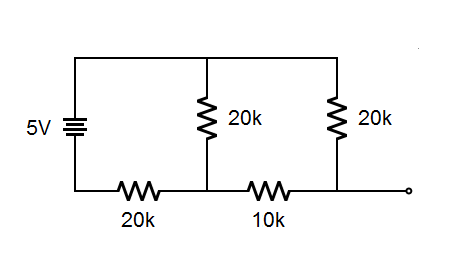 |
Again, look carefully, it is the same as the above circuit. Now let's analyze it:
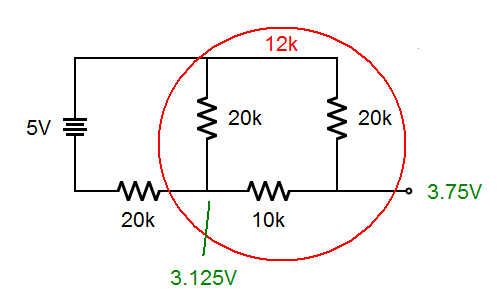 |
Like the circuit with binary 01 applied, we have 12k in series with 20k. This time the 12k is on the top, and the 20k is on the bottom. Using series circuits rules, we find there are 3.125 volts at the indicated node. The last 10k and 20k resistor act like a voltage divider giving us 3.75 volts on the output, which is the correct voltage.
We could analyze a four input R/2R ladder, but we won't. However, you can see that it works and all we need to do is build it to make it work.
One last thing, the feedback resistor is not critical to the basic operation of the circuit. This resistor can be changed to get the output voltage range you want. In fact, you could put the output of the R/2R ladder into a non-inverting amplifier as well as the inverting amplifier shown above. In the end, either circuit does the job of converting a digital input into an analog output, and it does it instantly.
| Vocademy |