| Vocademy |
AC Waveforms
In The Time Domain, we see how quantities that change over time can be illustrated using time domain graphs. Since alternating current has a voltage that repeatedly changes over time, we use time- domain graphs to illustrate AC waveforms.When we talk about AC waveforms, we are not talking about waves like ocean waves. An AC waveform is only a graph of how voltage changes over time. That often reminds us of waves like ocean waves. There are some definite relationships between AC waveforms and physical waves. However, AC waveforms are not things that take up space or move through space like ocean waves, sound waves, or radio waves. They are just illustrations of how voltage changes over time.
Let's take another look at the rotating battery model of alternating current.
 |
 |
| The rotating battery
model of an AC generator |
Here the current remains steady for a moment then suddenly reverses direction. It repeats this over and over as the battery rotates. Let's make a time-domain graph of this.
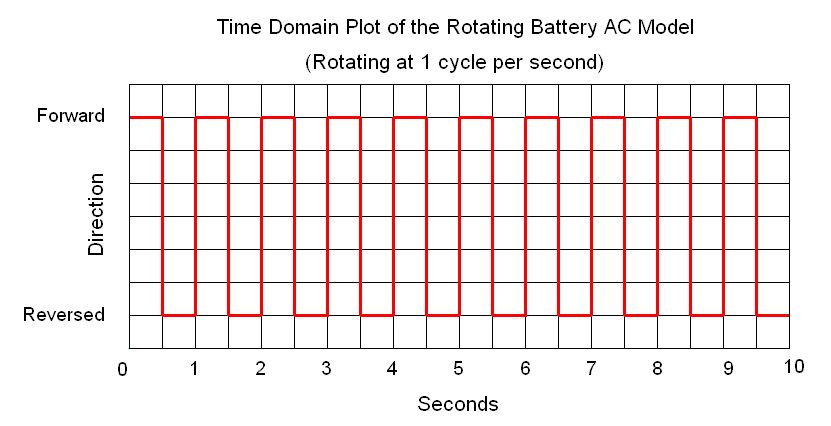
The "Forward" and
"Reversed" labels can be replaced with "Positive" and "Negative"
labels. Here the reversals are abrupt, as in flipping a switch back and
forth. Other AC waveforms make smooth changes such as a sine wave
(described below). There can be other patterns too as we will see below.
The AC delivered by the power grid is in the form of a sine wave. This is the natural result of rotating a magnetic field past coils of wire. AC is also created by electronic oscillator circuits. Theses produce AC waves of low power for various circuits such as sound generators, radio circuits and digital circuits. Function generators use oscillators to produce a variety of low power wave shapes for testing purposes. The usual waveforms available from a function generator are a sine wave, a triangle wave (which appears as repeated isosceles triangles in a graph) or a square wave (the time domain graph of the rotating battery above is a square wave). These waveforms each have certain characteristics that make them suitable for testing circuits. Another useful waveform is the sawtooth wave (the time domain plot of the clock hands in The Time Domain is a sawtooth wave). These are all described below.
The AC delivered by the power grid is in the form of a sine wave. This is the natural result of rotating a magnetic field past coils of wire. AC is also created by electronic oscillator circuits. Theses produce AC waves of low power for various circuits such as sound generators, radio circuits and digital circuits. Function generators use oscillators to produce a variety of low power wave shapes for testing purposes. The usual waveforms available from a function generator are a sine wave, a triangle wave (which appears as repeated isosceles triangles in a graph) or a square wave (the time domain graph of the rotating battery above is a square wave). These waveforms each have certain characteristics that make them suitable for testing circuits. Another useful waveform is the sawtooth wave (the time domain plot of the clock hands in The Time Domain is a sawtooth wave). These are all described below.
The Sine Wave
A sine wave makes a smooth transition as it reverses direction and is the most pure waveform possible. In fact, all other waveforms can be broken down into separate sine waves. A sine wave is mathematically related to a circle. Because of this, some of the same nomenclature used to describe and measure circles is also used for sine waves.Rotating Disk Model
One way to envision a sine wave is by imagining a spot on a rotating disk. Looking at the disk face-on the spot will move in a circle. Looking at the disk edge-on the spot will move up and down. If the disk is then moved uniformly along the rotational axis the spot will trace a sine wave. Another way to describe it is that a sine wave looks like a spiral seen edge-on.
 |
|
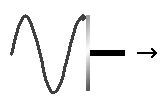 |
| A spot on
rotating disk |
Looking at
the disk edge-on, as the rotating disk moves along the rotational axis
the spot traces the shape of a sine wave |
There is a close relationship between the time domain graph of the angle of the clock hands and a sine wave. This graph showed the change in angle over time. If the graph is made with the trigonometrical sine of the angle instead of the angle in degrees, it would appear as a sine wave.
Parameters
There are four parameters used to measure sine waves: amplitude, phase, frequency and period.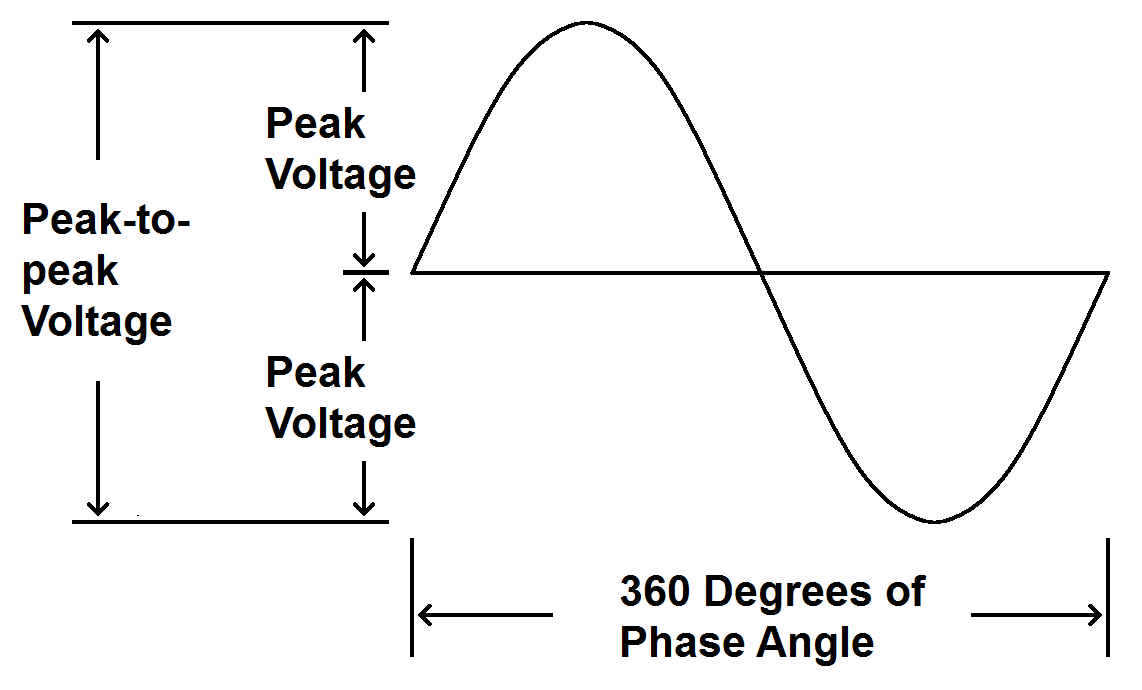
Amplitude
Amplitude represents how large the wave is. Amplitude can be any appropriate measurement (volts, amperes, watts, etc.). Amplitude is expressed in three different ways: Peak, peak-to-peak and RMS. The RMS value is not shown in the above diagram because it is a mathematical construct and can't be illustrated.Peak Voltage
Peak voltage is the Maximum deviation from the middle of the wave in either direction.Peak-to-Peak Voltage
Peak-to-peak voltage is the maximum voltage from one peak to the opposite peak, positive and negative. The peak-to-peak voltage is always twice the peak voltage.RMS Voltage
RMS (Root-Mean-Square) is a complex calculation that represents the DC voltage that would dissipate the same power as the AC voltage being measured. The calculation is made by sampling many voltages at even intervals during one cycle. The square-root is taken of each of these voltages. The arithmetic mean (the average) is calculated for the square-roots. Finally, this result is squared. This may sound a bit daunting but for sine waves (and only sine waves) the RMS voltage is simply 70.7% of the peak voltage. We rarely need the RMS value of other wave shapes. Most volt meters get the RMS value of an AC wave by sampling the peak voltage and use a voltage divider to present 70.7% of that peak voltage. If you do need the RMS value of something other than a sine wave you will use a "true RMS" volt meter.Phase
Let's take a look at a sine wave as it looks on an oscilloscope. The oscilloscope makes a graph of the voltage changes over time. In the image below, we see a wave with a period of 20 mS (which is a frequency of 50 Hz) and a peak voltage of about eight volts.
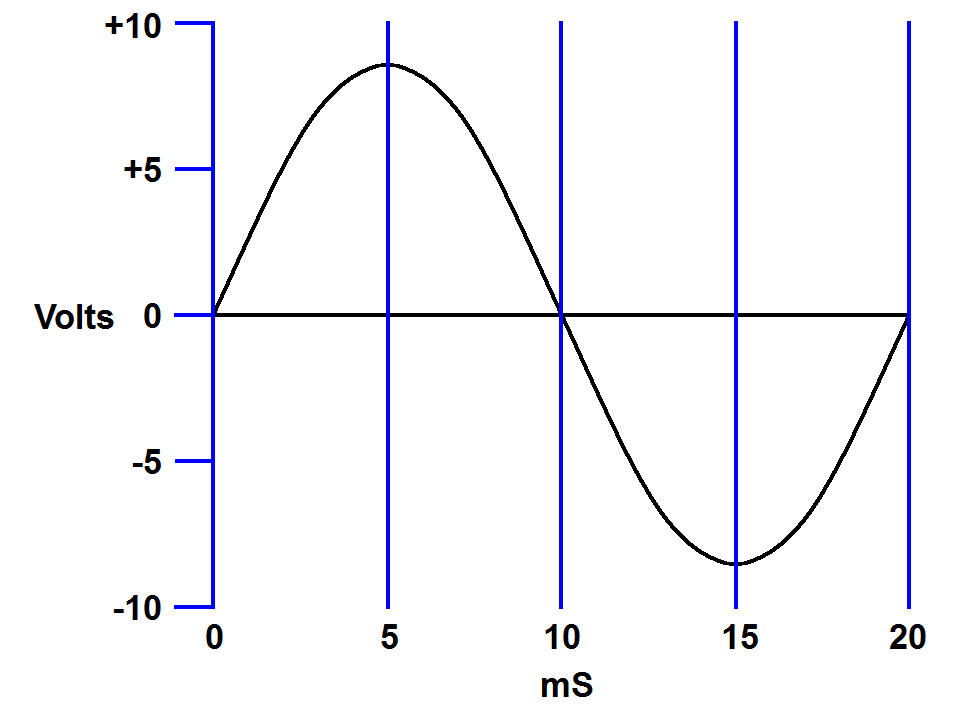 |
| A 50 Hz sine wave with a peak voltage of about 8 volts. |
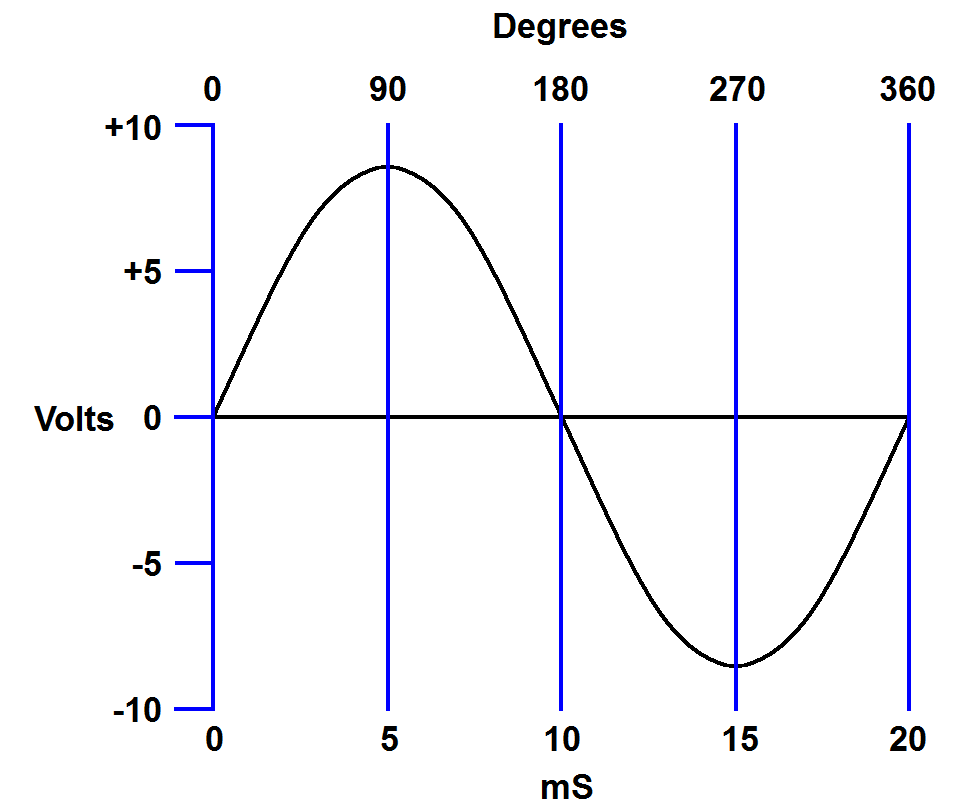
We have drawn this graph so that the wave is at 0 volts at 0 milliseconds. This is arbitrary, but where most people like to start. Now let's add a degree scale with 0 degrees lined up with 0 mS. Again this is arbitrary, but how most people line these parameters up.
 |
| Sine wave with degree scale |
We have set up our graph so that the wave starts with 0 volts at 0 degrees. The wave peaks at 90 degrees, crosses 0 volts again at 180 degrees, reaches its negative peak at 270 degrees then starts over at 360 degrees. Now let's add an identical wave, except lets have this one cross 0 volts 5 mS after the first wave.
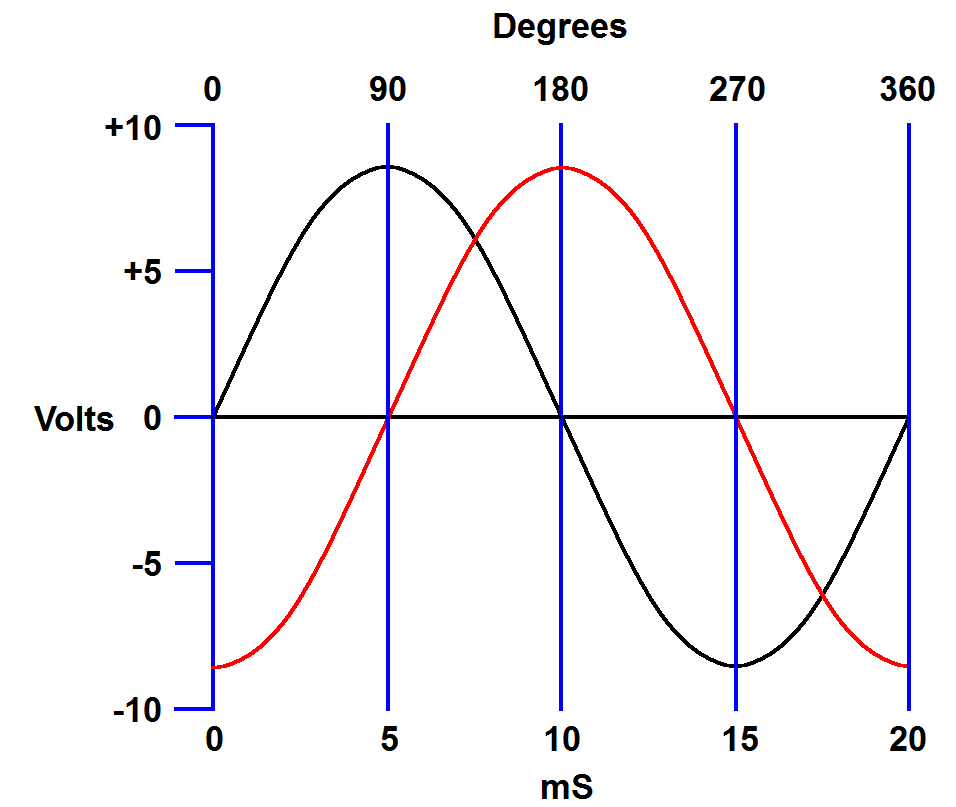 |
| Two sine waves 90-degrees out of phase. |
Notice that every event of the second wave (red) occurs 90 degrees after the same event of the first wave. In this case that is also 5 mS later, but that is only for this particular set of waves. If we remove the time and voltage scales we see that the waves are still 90-degrees out-of-phase even if we don't know the voltage or frequency.
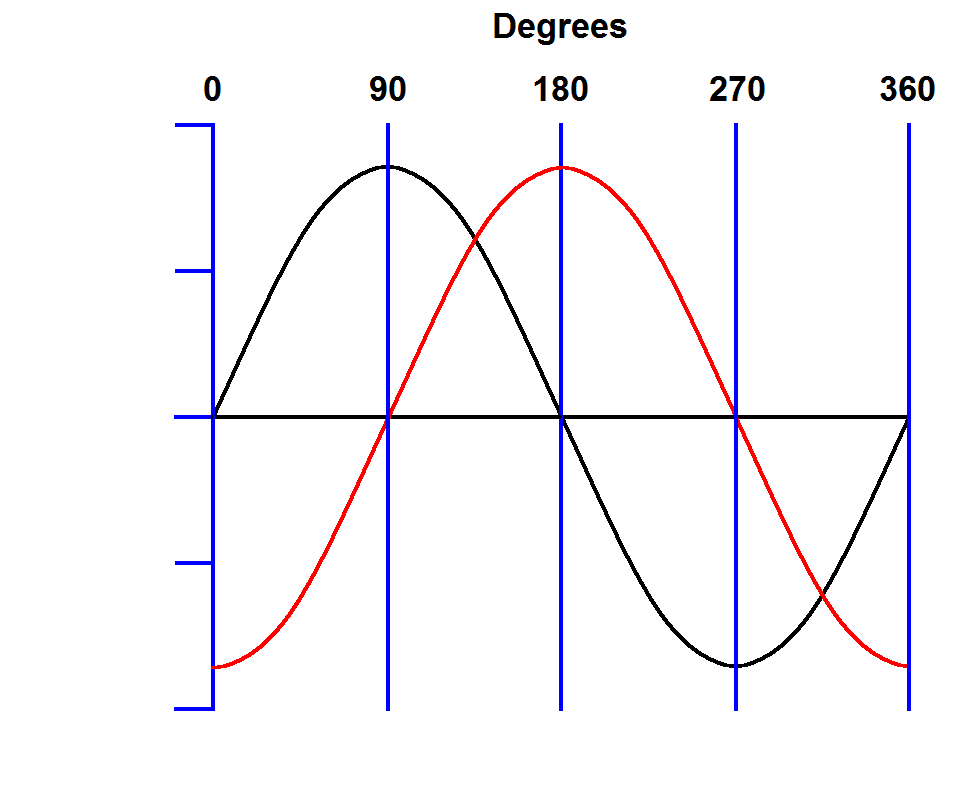 |
| Two sine waves 90-degrees out of phase. |
Here we have demonstrated how the term "phase" is used to compare two waves of the same frequency that happen at different times. The waves don't have to be the same amplitude. If they are different amplitudes one is just larger than the other. The phase relationship doesn't change.
Each cycle of a wave has 360 degrees and you have a different voltage at each point. The term phase may be used to specify a particular point along a wave, but is usually used when comparing one wave to another.
Frequency
Frequency is the number of times the wave completes one cycle in one second.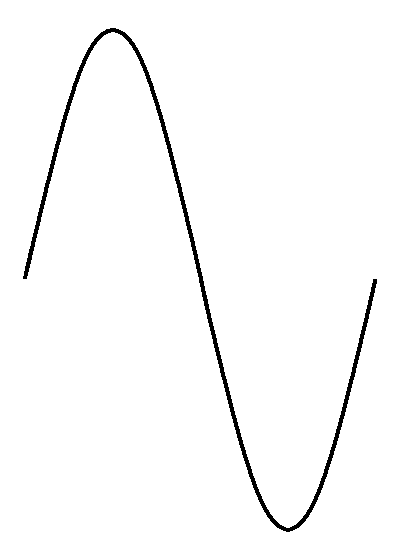 |
 |
 |
| Complete cycles of a sine wave,
a square wave (explained below) and a triangle wave (also explained
below). |
The above illustration shows one cycle of a sine wave, a square wave and a triangle wave. These are repeated over and over with alternating current. If you count how many times a wave repeats every second you have its frequency. Frequency is measured in Hertz (Hz) where 1 Hz equals one cycle per second, 20 Hz equals 20 cycles per second, etc. When we think of AC we usually think of the power coming from the power grid, such as that from a wall plug. The frequency here will be 50 Hz or 60 Hz depending on your location (more about that in power distribution). In electronic circuits you may have frequencies anywhere in a tremendous range. Audio frequencies (humans can hear vibrations in the air at audio frequencies) range from 20 Hz to 20,000 Hz (20 kHz). Ultrasonic frequencies (humans cannot hear vibrations in the air at ultrasonic frequencies) range from 20 kHz and above. Radio frequencies are those frequencies that are typically used for radio systems. These frequencies range anywhere from around 50 kHz (and overlap with ultrasonic frequencies) to billions of cycles per second.
Period
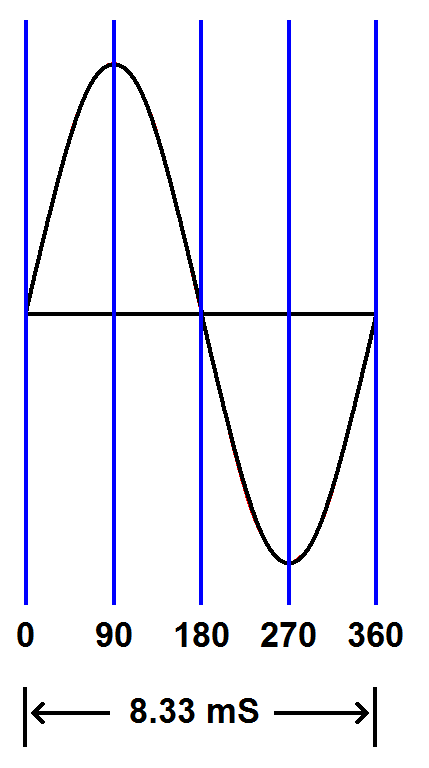
The period of a wave is the time it takes to complete one cycle. The illustrations below show two sine waves of different frequencies. Notice that the 120 Hz wave completes its cycle in half the time of the 60 Hz wave. The 60 Hz wave has a period of 0.0166 seconds (16.6 mS) and the 120 Hz wave has a period of 0.00833 seconds (8.33 mS). Notice that higher frequencies have shorter periods.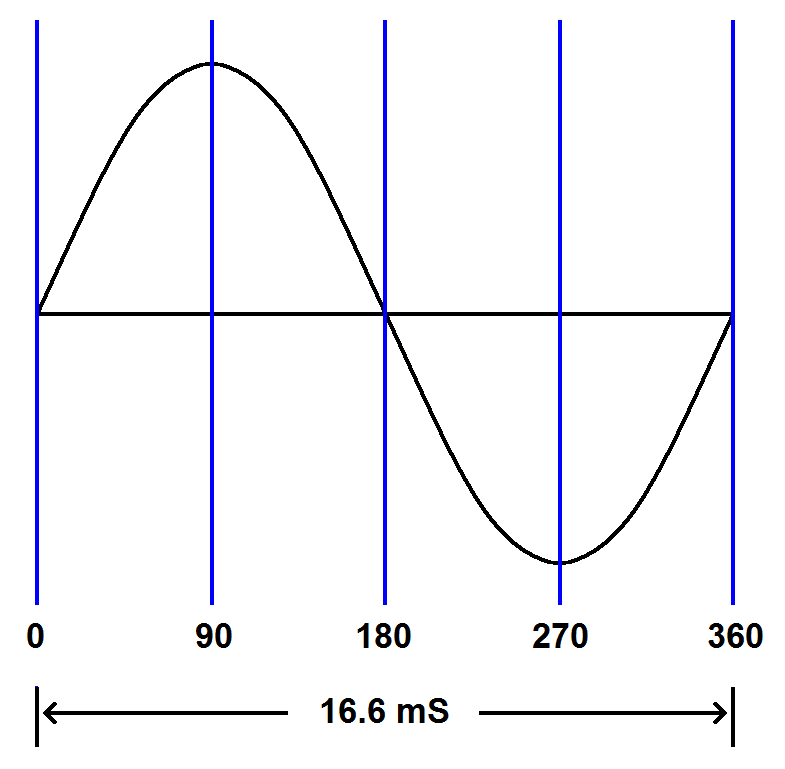 60 Hz |
|
 120 Hz |
| The 60 Hz sine wave on the left takes twice the time to complete one cycle as the 120 Hz sine wave on the right (16.6 milliseconds compared to 8.33 milliseconds). |
Mathematically the period is the reciprocal of the frequency and the frequency is the reciprocal of the period. For example, a 60 Hz wave has a period of 16.6 ms (1 ÷ 60 = 0.0166). Calculating frequency and period by reciprocals will be discussed later along with using the oscilloscope.
Wave Components
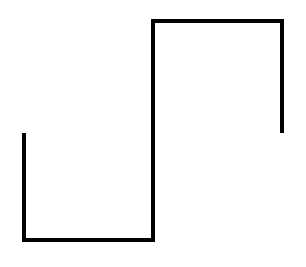
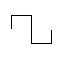
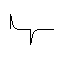
Square waves
Simply switching between two voltages (like turning a switch on and off) will produce a square wave. It is called a square wave because of the sharp, square edges when seen on a time domain graph.
| A time domain graph of a square
wave |
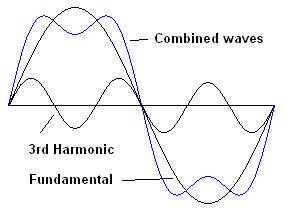
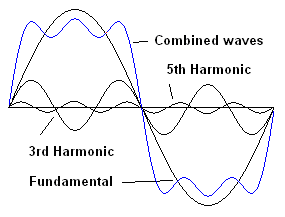
A square wave is easy to produce and may look simpler than a sine wave. Actually, a square wave is much more complex. It turns out that a square wave consists of a sine wave at the fundamental frequency of the wave plus all of the odd harmonics (harmonics are multiples of the fundamental frequency). For example 1 kHz square wave consists of a sine wave at 1 kHz. It also contains another sine wave at 3 kHz (the third harmonic), but of a smaller amplitude. It contains yet another sine wave at 5 kHz of yet smaller amplitude and so on. The following diagrams show the development of a square wave, starting with a sine wave and adding odd harmonics (watch the video at the bottom of this page to see various wave shapes built from sine waves).
 |
|
 |
|
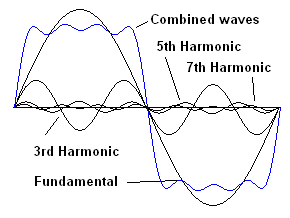 |
| Here we have a sine wave of a particular frequency (the fundamental). If we mix in another sine wave at three times the fundamental frequency (the third harmonic) they combine to make the blue wave. The sides of the resulting wave are steeper and the top is pulled down. | Adding the fifth harmonic steepens the sides more and starts to flatten the top | Adding the seventh harmonic steepens the sides even more and flattens the top more. |
If this process is continued, adding higher and higher harmonics, the wave becomes completely square. This shows how a square wave can be built by adding sine waves together. Square waves are useful for testing the bandwidth of circuits, i.e., testing if a circuit can pass a wide range of frequencies. A circuit with a wide bandwidth will pass a square wave undistorted. However, if the square wave comes out with a steep leading edge but a distorted trailing edge, the circuit can't handle the lower frequencies. If the square wave comes out with a steep trailing edge and a distorted leading edge, the circuit can't handle the higher frequencies.
The following example shows a circuit called a high-pass filter. It is designed to pass high frequencies but block low frequencies. In this case, the distorted square wave at the output (with a steep leading edge and a distorted trailing edge) shows that it is blocking low frequencies.
 |
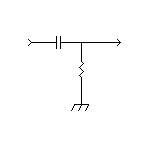 |
 |
 |
| Square
Wave |
High-pass
Filter |
Distortion
due to insufficient low frequency response. The diagram to the right has worse low frequency responese. |
|
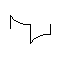
Triangle wave
Another wave shape you may encounter is a triangle wave. A triangle wave has symmetrical linear slopes leading to a peak as shown in the following diagram.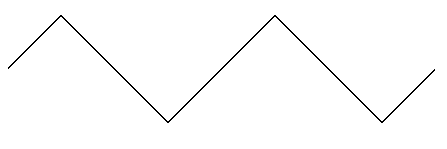
| A triangle wave |
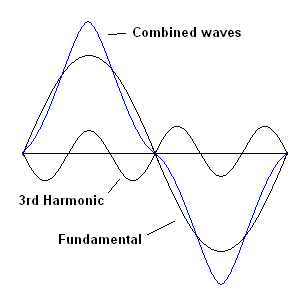
Like the square wave, a triangle wave is made up from the fundamental wave and all of the odd harmonics. However, each harmonic is 180 degrees out-of-phase (inverted) with the previous one.
 |
|
 |
| Here
the third harmonic is 180 degrees out of phase with the fundamental.
The sides of the combined waves are made less steep and the top
is heightened. |
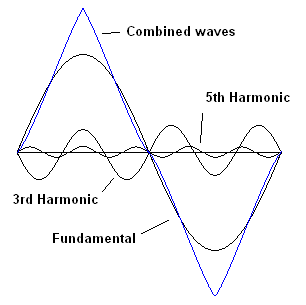
The
fifth harmonic is back in phase with the fundamental. It steepens the
sides and the top is heightened
even more. The wave is already a triangle wave with little distortion.
Adding more odd harmonics makes the sides straighter. |
Sawtooth wave
A sawtooth wave is a triangle wave where the slopes are not symmetrical, i.e. one slope is steeper than the other. Sawtooth waves were used in CRT-based televisions and computer monitors to control the movement of the scanning electron beam. For example, a sawtooth wave that rises slowly and drops quickly is used to move the electron beam slowly from left to right then quickly from back to the left.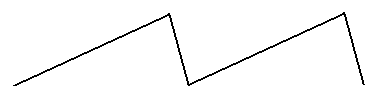
| A sawtooth wave |
A sawtooth wave is made up from the fundamental and all of the harmonics (both odd and even) where each harmonic is 180 degrees out of phase with the previous harmonic.
AC Waveforms
| Vocademy |