| Vocademy |
Inductors in AC Circuits
Inductive Reactance
Recall from the section on Inductors in DC Circuits that inductors are the opposite of capacitors in virtually every way. As the frequency of the alternating current increases, the opposition to current flow presented by a capacitor (capacitive reactance) decreases. With an inductor, it is just the opposite; as the frequency increases the opposition to current flow (inductive reactance) increases. At high-enough frequencies an inductor is a virtual open circuit. As opposed to capacitors, if you increase the value of an inductor, inductive reactance increases.Calculating Inductive Reactance
Like capacitive reactance, you need to be able to calculate the inductive reactance for a particular inductor at a given frequency based on the value of the inductor.The formula to calculate inductive reactance is:
XL = 2πƒL
Where:
| |
XL | = |
inductive reactance in ohms |
| 2π | = |
6.28 | |
| ƒ |
= |
frequency in hertz | |
| L | = |
capacitance in henrys |
The steps to solve this formula are:
- Multiply the frequency by 6.28
- Multiply the resulting product by the inductance.
When you apply a square wave to an inductor you get a curve that appears identical to the one you get with a capacitor. However, the voltage and current are reversed. You get a high peak of voltage on the leading edge of the square. The current starts at zero then climbs to its maximum. Meanwhile, the voltage drops to zero.
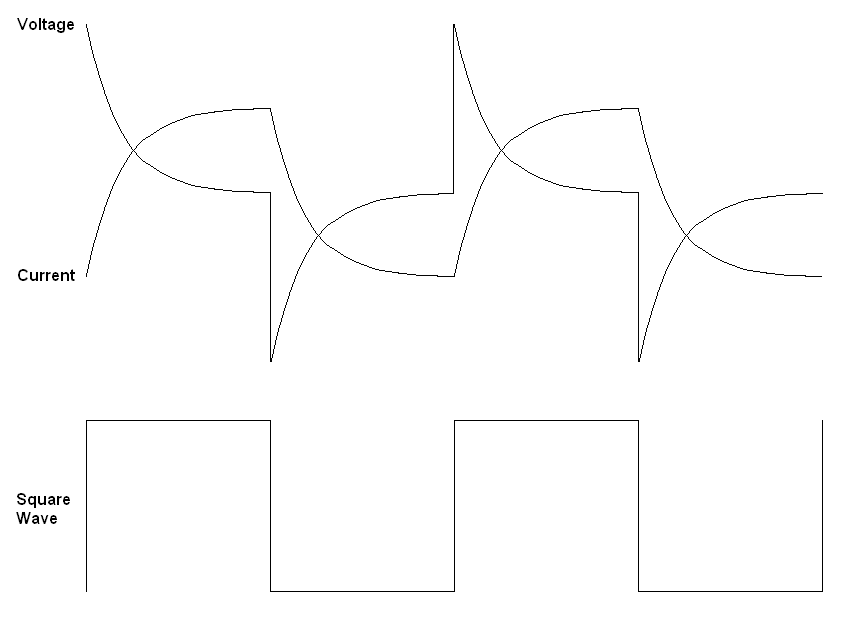
ELI
When AC is placed across an inductor there is a phase delay between voltage and current just as in capacitors. However, in an inductor the voltage leads the current. The acronym to remember this is ELI where E represents voltage, L represents an inductor and I represents current. To help remember the two acronyms think of ELI the ICE man. ELI reminds you that voltage leads current in an inductor and ICE reminds you that current leads voltage in a capacitor.
Inductors in AC Circuits
Inductors and Current - Answers to Questions
| Vocademy |