| Vocademy |
Math Review 1
Squares and Square Roots
A square is a number multiplied by itself. For example, 2 x 2 = 4. Therefore, 4 is the square of 2. Likewise, 5 x 5 = 25 and 10 x 10 = 100. Therefore, the square of 5 is 25 and the square of 10 is 100.A square can also be notated as a number raised to the power of 2 (raised to an exponent of 2). This is notated as 32 . Therefore, the square of 3 can be expressed as follows:
3 squared = 3 x 3 = 32
= 9
A square root is the opposite of a square. If 9 is the square of 3 then 3 is the square root of 9. Also, as in the examples above the square root of 25 is 5 and the square root of 100 is 10. The symbol for square root is √ .Therefore, the following expresses that the square root of 25 is 5:
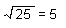
One practical use of squares and square roots is with the area of a square. If you take the mathematical square of the length of one side of a physical square you get the area of the square. The square root of the area of a physical square is the length of one side of the square. A square that is 10 inches on each side has an area of 100 square inches. Likewise, a square with an area of 100 square inches has four sides that are 10 inches long each.
Geometry of Right Triangles
A right angle is formed by two lines that meet at an angle of 90 degrees; a corner of a square forms a right angle. A right triangle is a triangle that has one angle that is 90 degrees, like a corner cut from a square.Right angle geometry comes into play when working with AC circuits. When inductors, capacitors and resistors work together in circuits, the timing of the voltage and current across the components (phase angle) are such that right triangle geometry can be used to analyze the relationships.
The primary formula for working with right triangles is known as the Pythagorean Theorem. This theorem first names the three lines that make up the right triangle. One of the two lines that form the right angle is called the base. The other line that forms the right angle is called the adjacent. The line that joins these two lines is called the hypotenuse.
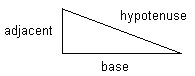
| The lines of a right triangle |
The Pythagorean Theorem is stated as follows:
The square of the hypotenuse is equal
to the sum of the squares of the other two sides.
To find the length of the hypotenuse:- Find the square of the length of the base
- Find the square of the length of the adjacent
- Add these squares together
- Find the square root of the sum
For example:
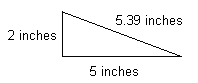
In this example:
- 5 squared (52 or 5 X 5) = 25
- 2 squared (22 or 2 X 2) = 4
- 25 + 4 = 29
- The square root of 29 (√29) = 5.39
To calculate this on a scientific calculator, use the following keystrokes (The last number, without the gray background is the answer. You don't type that in.) :
| 5 |
X2 |
+ |
2 |
X2 | = |
√ | 5.39 |
|||||||
| press these keys |
displayed answer |
|||||||||||||
Complex Numbers
A complex number is two numbers that are added together after multiplying one of the numbers by the square root of -1. This isn’t as daunting as it might sound. First of all, the square root of -1 is represented by the lower-case letter i. So a complex number looks like the following:A + iB
A complex number
A complex number
Complex numbers are useful in electronics because they can be used to describe right triangles. The right triangle above can be notated as:
5 + i2
The complex number simply says "Go 5 units, turn right then go 2 units". If the triangle is flipped, as follows:
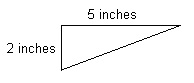
This triangle can be notated as:
5 - i2
This can be interpreted as "Go 5 units, turn left then go 2 units". +i means turn right and -i means turn left.
In electronics, to avoid confusing complex numbers with the symbol for current the lower case j is used in place of the lower case I. If the above triangles were being used to analyze an AC circuit, they would be notated as follows:
Complex numbers using j instead of i.
| 5 + j2 | 5 - j2 | |
| First Triangle | Second Triangle |
When AC circuits are expressed with complex numbers it is called rectangular notation. In this case, the base of the triangle represents resistance and the adjacent represents capacitive reactance or inductive reactance. Capacitive reactance is represented by - j and inductive reactance is represented by + j. Since inductive reactance and capacitive reactance cancel each other and +j and -j also cancel each other — for example (+ j10) + (- j10) = 0 — complex numbers facilitate adding capacitive reactance and inductive reactance.
Sine, cosine and tangent
Describing two sides of a right triangle with rectangular notation is sufficient to describe the whole triangle. Another way to describe a right triangle is to describe the length of the hypotenuse and the angle between the hypotenuse and the base. This is called polar notation and is also useful when working with AC circuits. The triangle above would be described in polar notation as follows: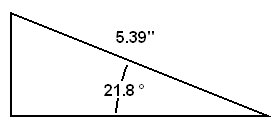
| The triangle from above described with polar notation. |
To convert from polar notation to rectangular notation, you need to find the sine and the cosine of the angle between the base and the hypotenuse.
Sine
The sine of an angle is the length of the adjacent divided by the length of the hypotenuse as shown in the following formula (θ, the Greek letter Theta represents an angle):| sin θ
= |
a |
| ————— | |
| h |
In our current example the adjacent is 2 inches and the hypotenuse is 5.39 inches. This gives us 2 ÷ 5.39 which is 0.371. Therefore, the sine of an angle of 21.8 degrees is 0.371. This is true no matter what the actual lengths of the sides are.
The adjacent is the length of the hypotenuse multiplied by the sine of the angle.
a = h x sin θ
Before pocket calculators, mathematicians would find the sine of an angle by looking it up in a book of tables. Today, all you have to do is press the [sin] button on a calculator. To calculate the length of the adjacent of the preceding triangle, use the following sequence:
| 2 |
1 |
. |
8 |
sin |
X |
5 |
. |
3 |
9 |
= |
2 |
This will give the answer of 2 inches.
Cosine
The cosine of an angle is the length of the base divided by the length of the hypotenuse. In this example that is 5 ÷ 5.39 which is 0.928. Therefore, the cosine of an angle of 21.8 degrees is 0.928.Multiplying the cosine of the angle by the length of the hypotenuse gives you the length of the base.
b = cos θ x h
Therefore, to calculate the length of the base of the preceding triangle, use the following sequence:
| 2 |
1 |
. |
8 |
cos |
X |
5 |
. |
3 |
9 |
= |
5 |
This will give the answer of 5 inches.
In review, if you have the length of the hypotenuse of a triangle and the angle between the hypotenuse and the base, you can calculate the lengths of the adjacent and the base with two simple formulas. The length of the base is the length of the hypotenuse multiplied by the cosine of the angle and the length of the adjacent is the length of the hypotenuse multiplied by the sine of the angle.
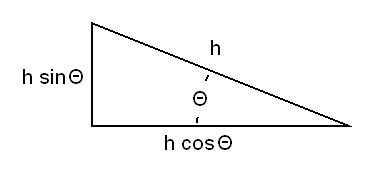
| Relationships of the sides of a
right triangle. |
Tangent
The tangent of an angle is the length of the adjacent divided by the length of the base. In the example, that is 2 ÷ 5 which is 0.4. Therefore, the tangent of an angle of 21.8 degrees is 0.4.Arcsine, arccosine and arctangent
These are simply the reverse (actually the inverse) of the sine, cosine and tangent. The arcsine of 0.371 is 21.8 degrees, the arccosine of 0.928 is 21.8 and the arctangent of 0.4 is 21.8 degrees.Most calculators label the arcsine button with sin-1, arccosine with cos-1 and arctangent with tan-1. Often you must press an "inverse" button before using these buttons. For example, to find the arcsine you may have to press [inv] then [sin]. Once again, be sure to familiarize yourself with your own calculator.
Conversion between polar and rectangular notation
You now have the tools to convert between polar and rectangular notation.To convert from rectangular notation to polar notation, first use the Pythagorean theorem to find the length of the hypotenuse. Then, divide the adjacent by the base and find the arctangent of the result. Therefore, in the current example, the rectangular notation is 5 + j2, where 5 is the base and 2 is the adjacent. To convert this to polar notation, use the following sequence.
| 5 |
X2 |
+ |
2 |
X2 |
= |
√ | 5.39 |
This gives you the length of the hypotenuse which is 5.39 inches.
Next, divide the adjacent by the base then find the arctangent of the result:
| 2 |
÷ |
5 |
= |
tan-1 |
|
21.8 |
This gives you the angle between the base and the hypotenuse, which is 21.8 degrees.
To convert from polar notation to rectangular notation:
- Find the length of the base by multiplying the length of the hypotenuse by the cosine of the angle
- Find the length of the adjacent by the multiplying the length of the hypotenuse by the sine of the angle
| 2 |
1 |
. |
8 |
sin |
X |
5 |
. |
3 |
9 |
= |
5 |
and
| 2 |
1 |
. |
8 |
cos |
X |
5 |
. |
3 |
9 |
= |
2 |
Which gives you 5 and 2 respectively which in polar notation is 5 + j2
Vectors
A vector represents a value using an arrow with a length that is proportional to that value. This arrow points in a particular direction showing that the value has something to do with direction. By definition, a vector is quantity that has both magnitude and direction. For example I can represent walking 100 feet to the north by drawing an arrow that is 100 mm long and points to the top of the paper. Two vectors can be combined to get a third vector that represents the result of the first two values. For example, let's say that after walking 100 feet to the north I turn right and walk 100 feet to the east. I can represent this action by drawing another arrow from the point of the first that goes 100 mm to the right. The result is as if I had walked 141 feet to the northeast. The third vector would be an arrow that starts at the same place as the first and goes 141 mm at a 45 degree angle.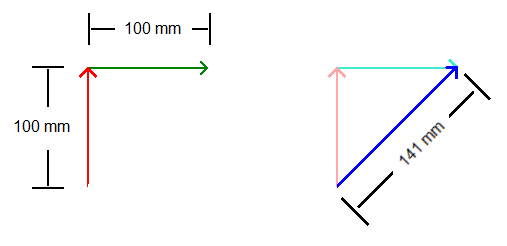
| If you walk 100 feet north then
100 feet east you end up in the same place as if you walked 141 feet
northeast. "The above vectors represent the trip using millimeters to
represent
feet. |
For another example, assume an airplane is flying on a heading of 0 degrees (northward) at 200 mph. The magnitude of the vector is 200 mph and the direction is 0 degrees. If the wind is blowing at 50 mph to the east (90 degrees) the airplane will be blown off-course. You can see how far the plane is blown off-course by drawing vectors on a grid. For example, you can draw an arrow along one line that is 20 squares long, representing 200 mph to represent the speed and direction of the airplane. At the point of this arrow you can draw another arrow pointing to the right with a length of 5 squares representing 50 mph. The point of this arrow will represent the position of the airplane after flying under these conditions for one hour. The airplane has will go 200 miles to the north and 50 miles to the east, ending up 50 miles east of where the pilot expected.
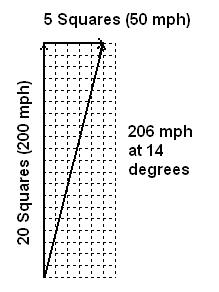
| Using vectors to plot the course of an airplane |
If you draw a line between the starting point and the ending point you will get the actual course the airplane traveled. Using a ruler and protractor you can measure the length of this line and the angle from the intended course. In this example the airplane traveled over the ground at a speed of 206 mph on a course of 14 degrees east.
As shown above, you can calculate the distance the airplane actually traveled using the Pythagorean theorem. The actual course can be calculated with trigonometry. In this case, to find the angle of the hypotenuse of the triangle (the actual course), divide the wind speed (the adjacent of the triangle) by the airplane speed (the base of the triangle) then calculate the arctangent of the result. This gives an angle of approximately 14 degrees.
| course
= arctan |
wind speed |
| ————————————— | |
| airplane speed |
On the calculator that would be:
| 5 |
0 |
÷ | 2 |
0 |
0 |
= |
tan-1 |
14 |
Which gives an angle of 14 degrees.
Using vector analysis is just a rework of the trigonometry that was already covered. The interaction of resistance, capacitive reactance and inductive reactance in an AC circuit can be analyzed using vectors. There are other aspects of electronics that can be analyzed with vectors too, such the interactions of different frequencies.
| Vocademy |