| Vocademy |
Impedance
Impedance is the combination of all the resistance, capacitive reactance and inductive reactance in a circuit. It is represented by the letter Z. As noted above, capacitive reactance and inductive reactance cancel each other in a series circuit. For example, assume you have 30 ohms of inductive reactance and 10 ohms of capacitive reactance. The 10 ohms of capacitive reactance will cancel 10 of the ohms of inductive reactance. This leaves 20 ohms of inductive reactance for the circuit total.Resistance does not combine directly with either inductive reactance or capacitive reactance. Resistance and reactance can be represented by vectors placed at right angles to each other. You can represent resistance (R) as the base of a right triangle and reactance (X) as the adjacent of the triangle. Impedance (Z) is then represented by the hypotenuse of the triangle.
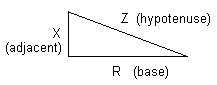
Impedance can be calculated by plotting the resistance and reactance on graph paper then measuring the length of the hypotenuse. Mathematically is can be calculated by using the Pythagorean theorem. This is expressed in the following formula.
h2 = s12 + s22
| h | = |
The hypotenuse (impedance in ohms) | |
| |
s1 | = | The base (resistance in ohms) |
| s2 | = | The adjacent (reactance in ohms) |
The above formula for the Pythagorean theorem can be reduced to the following formula for calculating impedance.
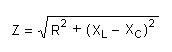
The steps to solve this formula are:
- Subtract capacitive reactance from inductive reactance
- Square this value and set it aside
- Square the resistance
- Add this value to the value set aside above
- Take the square-root
| 5 | 0 |
- |
3 | 0 |
= |
X2 |
MS |
1 |
0 |
0 |
X2 | M+ |
MR |
√ | 101 |
Following the above steps this is what these keystrokes are doing (your calculator may be different):
- Subtract XC from XL (50 – 30 =)
- Square the result (X2)
- Store the above in memory (MS)
- Square the resistance (100 X2)
- Add this square to memory (M+)
- Retrieve the sum of the squares from memory (MR)
- Get the square root ( √ )
The result is a positive number, meaning that the reactance in the circuit is predominantly inductive. However, after capacitive reactance is subtracted from inductive reactance, the remaining reactance is much less than the resistance. Since resistance is the dominant factor of the impedance, the circuit is a resistive circuit. If, the reactance were the dominant factor, the circuit would be reactive. At a given frequency, a circuit is either resistive, capacitive or inductive, depending on which is dominant after subtracting the capacitive reactance from the inductive reactance.
Phase angle
As explained above, voltage and current do not change together in capacitors and inductors. In a capacitor, the voltage always lags behind the current; in an inductor the current always lags behind the voltage. This delay is called phase angle. In capacitors and inductors, whatever the frequency this lag is always 90 degrees. This essentially means that, in a capacitor, when the current is at the peak the voltage is at zero, when the voltage reaches the peak the current is at zero. By the time the voltage also drops to zero the current has changed direction and has reached its peak in the opposite direction. When the voltage also reaches its opposite peak, the current is at zero again. Voltage will always chase the current in this manner.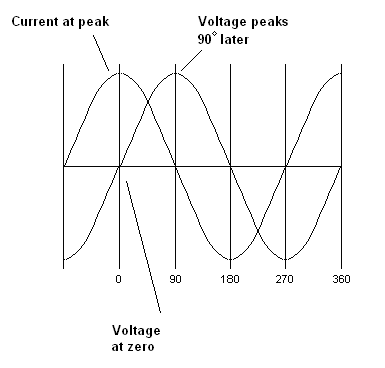
| Current and voltage with a capacitor |
In a resistor the voltage and current are always in phase; when the current peaks so does the voltage. In a series circuit the current is always the same. When you have a resistor and a capacitor in a series AC circuit, the voltage across the capacitor will be 90 degrees out-of-phase with the voltage across the resistor. Keep in mind that Kirchhoff's voltage law still applies. At any moment in time the voltages across the resistor and capacitor will add up to the voltage at the AC source (generator, oscillator, etc.) at that moment.
With the voltages out-of-phase the total opposition to current flow (the impedance) is not the direct product of voltage divided by the current. The phase angles have to be factored in. The total phase angle factor is a trigonometric function as follows:
| phase angle = arctan |
reactance |
| —————————— | |
| resistance |
For example, if a circuit has a resistance of 200 ohms and at a particular frequency a capacitive reactance of 50 ohms, the phase angle would be calculated as follows on a typical calculator:
| 5 |
0 |
÷ | 2 |
0 |
0 |
= |
tan-1 |
14 |
Which gives a phase angle of 14 degrees.
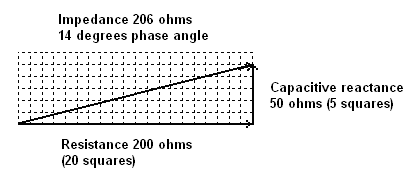
| Impedance plot with 50 ohms of capacitive reactance and 200 ohms of resistance. |
Rectangular notation
The above example uses polar notation. It represents the impedance as a vector—a quantity and a phase angle. Impedance can also be expressed in rectangular notation. Here is the above impedance expressed in rectangular notation:
200 - j50
This denotes 200 ohms of resistance and 50 ohms of reactance. The - j (negative number) indicates capacitive reactance. Inductive reactance uses + j (positive number). When worked together, inductive reactance and capacitive reactance cancel each other.
The Pythagorean theorem is used to convert form rectangular notation to polar notation along with the previous phase angle formula. To convert polar notation to rectangular notation, the impedance is multiplied by the sine of the angle to get the reactance and by the cosine of the angle to get the resistance.
sin 14 X 206 = 50 (the reactance) cos 14 X 206 = 200 (the resistance)
AC Basics - Why AC Circuits Have a Phase Angle
| Vocademy |