| Vocademy |
Filters
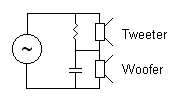
Electronic circuits can work over a wide range of frequencies, anywhere from DC (zero hertz) to billions of cycles per second (gigahertz). It is often desirable to limit the range of frequencies that a circuit responds to. Filters are used to limit the frequency response of a circuit.A typical use of a filter circuit is a crossover network in a speaker system. It is difficult to make a single loud speaker that responds to the full range of audio frequencies. A woofer, a speaker that responds to low frequencies must be large and able to move a lot of air. This is just the opposite of a tweeter, a speaker that responds to high frequencies. It must be small and light so that it can vibrate at high frequencies. The output of a high fidelity audio amplifier will respond to the full range of audio frequencies. You could simply put a woofer and tweeter in parallel. However, high frequencies reaching the woofer are wasted energy. Low frequencies reaching the tweeter can cause it to overheat. A crossover network is a filter that directs high frequencies to the tweeter and low frequencies to the woofer. The circuit used in the example below is not a practical crossover network because it has a resistor as part of the filter. Power is produced in resistors which is a waste energy. A practical crossover network is made of only capacitors and inductors. Such LC filters will be seen later in this section. Practical crossover networks will be discussed in analog circuits.
RC Filters
In a circuit made of a single resistor and a single capacitor there is a frequency where the resistance and capacitive reactance will be equal. This frequency is called the cutoff frequency (ƒCO). Looking at the following circuit, at frequencies below the cutoff frequency more voltage is developed across the capacitor than the resistor. At frequencies above the cutoff frequency more voltage is developed across the resistor than the capacitor. If you were using this filter as a crossover network you would want the tweeter across the resistor and the woofer across the inductor.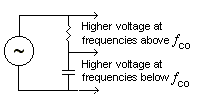 |
 |
An RC filter would not be used as a practical crossover network because the resistor would waste power. RC filters are used in the low power parts of a circuit, such as at microphone inputs and between preamplifiers and power amplifiers.
Another definition of the cutoff frequency is the half-power point. At the cutoff frequency the power produced across the resistor and the capacitor are equal. Therefore, 50% of the power is across each of the two components. If the filter is seen as having an input and an output (see below for further explanation), 50% of the power is reaching the output.
Low pass RC Filter
In the above arrangement, the voltage across the resistor or the capacitor can be isolated and used to connect to another circuit. For example, the output of an audio preamplifier may be placed across both components, the components seen as in series from the preamplifier. The voltage developed across either the resistor or the capacitor can be sent to the input of another amplifier stage. The connection across both components is then considered the input of the filter and the connection a single component is considered the output of the filter.If the connection across the capacitor is used as the output of the filter a higher voltage will be developed at frequencies below the cutoff frequency. Low frequencies will be passed through the filter at a higher level than high frequencies. This arrangement constitutes a low pass filter.
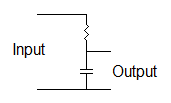
| A low pass
filter |
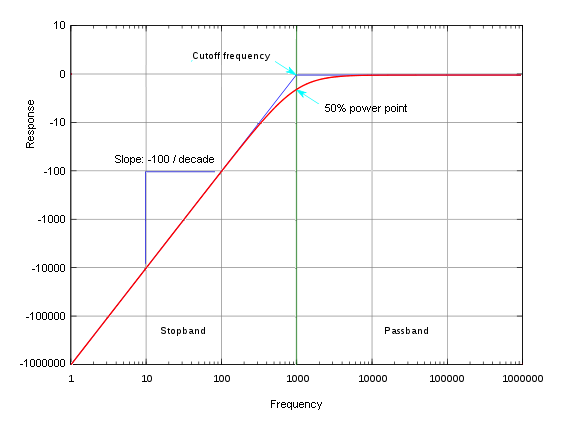
The following diagram shows a typical power output plot of a low pass filter. The grid is laid-out using a mathematical function called a logarithm (discussed later in analog circuits). This distorts the appearance of the plot in such a way that it appears as a flat line at frequencies below the cutoff frequency and as a straight sloped line at frequencies above the cutoff frequency. This makes a visual graph that is easier to interpret than the continuously-curved lines that would appear in a linear function (with evenly spaced intervals) were used. It also distorts the graph in such a way that the half-power point appears to be much higher than you might expect. The frequency shown is relative; the 1000 doesn't necessarily represent 1,000 Hz. The actual cutoff frequency depends on the components.
This plot illustrates the response of a low pass filter. The output is unaffected by the filter at frequencies below the cutoff frequency but drops off dramatically at frequencies above the cutoff frequency. This particular plot drops of by a factor of 100 for every ten-fold increase in frequency. This would be referred to as -100 per decade.
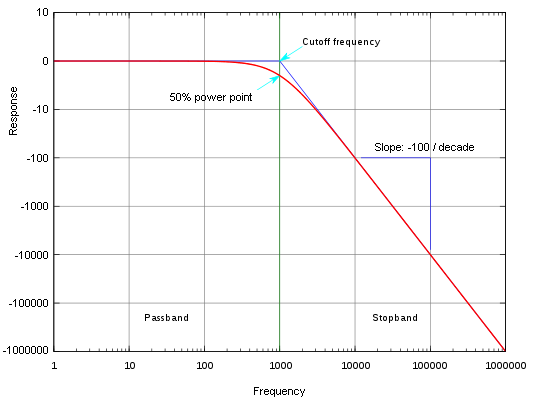
|
Response of a low pass filter
The frequency is relative. The slope depends on the filter design. The response of a typical filter is in red. The purple line is a bode plot, which is a straight-line approximation of a filter response. The grid is plotted using a logarithmic function (decibels [dB]). This is why the half-power point appears to be much greater than 50% of the maximum level. Logarithms and decibels will be discussed in analog circuits. |
Let's build a formula to find the cutoff frequency of an RC filter. At the cutoff frequency the capacitive reactance equals the resistance.
XC = R
| At the
cutoff frequency |
Therefore, the resistance equals the formula for capacitive reactance:
| R
= |
1 |
| ——————— | |
| 2πƒC |
| At the
cutoff frequency |
Using the rules for the basic algebraic formula we can pull the frequency out and solve for it:
| ƒ
= |
1 |
| ——————— | |
| 2πRC |
| At the
cutoff frequency |
Since this only works at the cutoff frequency the frequency solved for is the cutoff frequency. This gives us the following formula to find the cutoff frequency:
| ƒCO
= |
1 |
| ——————— | |
| 2πRC |
Where:
|
|
ƒCO
|
= |
cutoff frequency |
| 2π | = |
Mathematical constant of 6.28 | |
| R |
= |
Resistance in ohms | |
| C |
= |
Capacitance in
farads |
For example, a 0.16 microfarad capacitor will have approximately 100 ohms of capacitive reactance at 10 kHz. If you make an RC filter using this 0.16 microfarad capacitor and a 100 ohm resistor the cutoff frequency will be 9,952Hz, which rounds to 10,000 Hz. χ
1/χ
| ƒCO
= |
1 |
≈ 10,000 |
| ————————————————————— | ||
| 6.28 x 100 x 0.00000016 |
| 6 |
. |
2 |
8 |
X |
1 |
0 |
0 |
X |
. |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
6 |
= |
1/χ | 9952... |
An RC filter is typically illustrated with the following configuration. Since the resistor and capacitor are drawn in the shape of the letter “L” it is called an “L” filter.
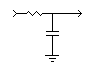
| An RC "L"
low pass filter |
A low pass filter is used in audio circuits where more bass response is desired. Radio circuits sometimes produce harmonic frequencies above the desired radio frequency. A low pass filter may be used to pass the desired frequency or range of frequencies while blocking the harmonics. The ripple filter of a power supply (discussed in analog circuits) is a low pass filter.
High pass RC Filter
The second circuit is the same as the low pass filter above except the
output is taken across the resistor.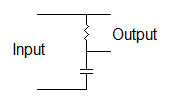
| A high pass
filter |
This makes it a high pass filter. Everything else applies the same as to the low pass filter. A high pass RC filter is typically drawn as below. As above it is drawn in the shape of the letter "L" and is called an "L" filter.
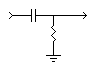
| An RC high pass "L" filter. This drawing is "flipped" compared to the previous one, but the filter works the same. The output is still across the resistor where the higher voltage is developed at higher frequencies. |
Like the low pass filter, increasing the value of the capacitor or the resistor will lower the cutoff frequency. The frequency response plot for a high pass filter is a "mirror image" of the plot for a low pass filter.
|
Response of a high pass filter
This is a mirror image of the
low pass filter graph.
|
High pass filters are used in audio circuits where more treble response is desired or in radio circuits where unwanted frequencies are below the desired frequencies.
LC Filters
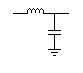
LC filters have the advantage of not wasting energy as by dissipating power in a resistor. Notice that in an LC filter you actually have a resonant circuit.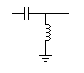 |
|
 |
| LC
high pass "L" filter |
LC
low pass "L" filter |
Therefore, the cutoff frequency will be the resonant frequency. At frequencies above the resonant frequency the inductive reactance is greater than the capacitive reactance. This creates a voltage divider where the voltage across the inductor is higher than the voltage across the capacitor. At frequencies below the resonant frequency the capacitive reactance is greater than the inductive reactance. The voltage across the capacitor is higher than the voltage across the inductor.
High pass filter
If the output is taken across the inductor of an LC filter you have a high pass filter. Another way to look at it is that higher frequencies pass through the capacitor to the output and lower frequencies go through the inductor to ground, bypassing the output.Low pass filter
If the output is taken across the capacitor of an LC filter you have a low pass filter. Another way to look at it is that the lower frequencies pass through the inductor to the output and the higher frequencies go through the capacitor to ground, bypassing the output.Band pass filter
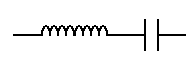
A band pass filter is designed to pass a range of frequencies. A series resonant circuit acts as a short circuit at the resonant frequency so it passes the resonant frequency and blocks higher and lower frequencies.| Input |
 |
Output |
|
A series band pass filter
Frequencies above and below the resonant frequency are blocked. Frequencies near the resonant frequency pass through. This filter is in series with the signal. |
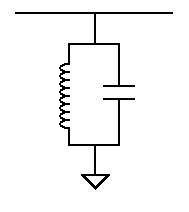
A parallel resonant circuit has a very high impedance it the resonant frequency. If you place a parallel resonant circuit across the signal path frequencies above and below the resonant frequency will be shorted out. Only frequencies near the resonant frequency will pass by the circuit and reach the output.
| Input |
 |
Output |
|
A parallel band pass filter
Frequencies above and below the resonant frequency are shorted to ground. Frequencies near the resonant frequency bypass the circuit. This filter is parallel or "across" the signal. |
A band pass filter can be made with a series or parallel resonant circuit. Which circuit is used depends on the orientation of the filter.
Band-reject filter
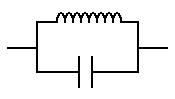
A band-reject filter (or notch filter) is designed to block a range of frequencies. These are made the same way as a band pass filter except for the orientation of the filter circuit. A parallel circuit in series with the signal operates as a band reject filter.| Input |
 |
Output |
|
A band reject filter using a parallel resonant circuit
Frequencies near the resonant frequency are blocked. Frequencies above and below the resonant frequency pass through the circuit. |
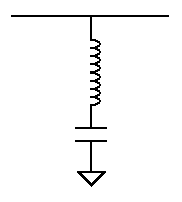
A series circuit across the signal path also operates as a band reject filter.
| Input |
 |
Output |
|
A band reject filter using a series resonant circuit
Frequencies near the resonant frequency are shorted to ground. Frequencies above and below the resonant frequency bypass the circuit. |
"Pi" Filters and "T" Filters
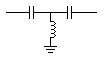
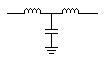
The previous filters are called “L” filters because the components are usually illustrated with the components laid out in the shape of the letter “L”. The “T” filter is usually illustrated with the components in the shape of the letter “T”. “T” filters can have any combination of components and be either low pass or high pass filters."T" filters
 |
|
 |
| LC
high pass "T" filter |
LC
low pass "T" filter |
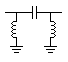
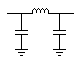
"Pi" Filters
 |
|
 |
| LC
high pass "Pi" filter |
LC
low pass "Pi" filter |
"H" filters
"T" and "Pi" filters are unsymmetrical. One end is ties to ground and the electrical signal they operate on is carried by a single wire (an unbalanced signal). Often electrical signals are carried by pairs of wires where the voltage in each wire is always opposite to the voltage in the other. This is a balanced signal and requires symmetrical or balanced filters. The most common balanced filter is the "H" filter. This is a balanced version of the "T" filter and is drawn resembling the letter "H".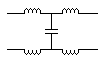 |
| LC
low pass "H" filter |
Narrow band and wide band filters
In the section on resonant circuits you can see that resonant circuits can be designed to have a sharp peak (high Q) or a shallow peak (low Q [review resonant circuits]). A high Q filter is a narrow band filter.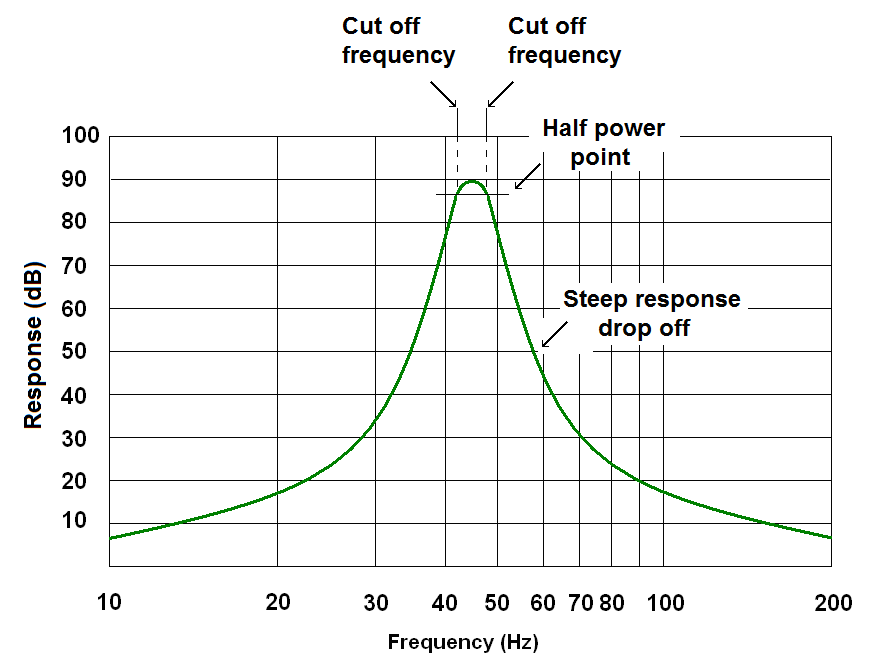
|
A high Q filter
The pass band of a high Q filter (the range of frequencies between the cutoff frequencies) is narrow. The drop off above and below the pass band is steep; the response of the filter drops off rapidly as you go above and below the pass band. |
The sharp drop off (steep skirts) of a high Q filter is often desirable, but it only passes a narrow range of frequencies. To pass a wide range of frequencies you need a low Q filter.
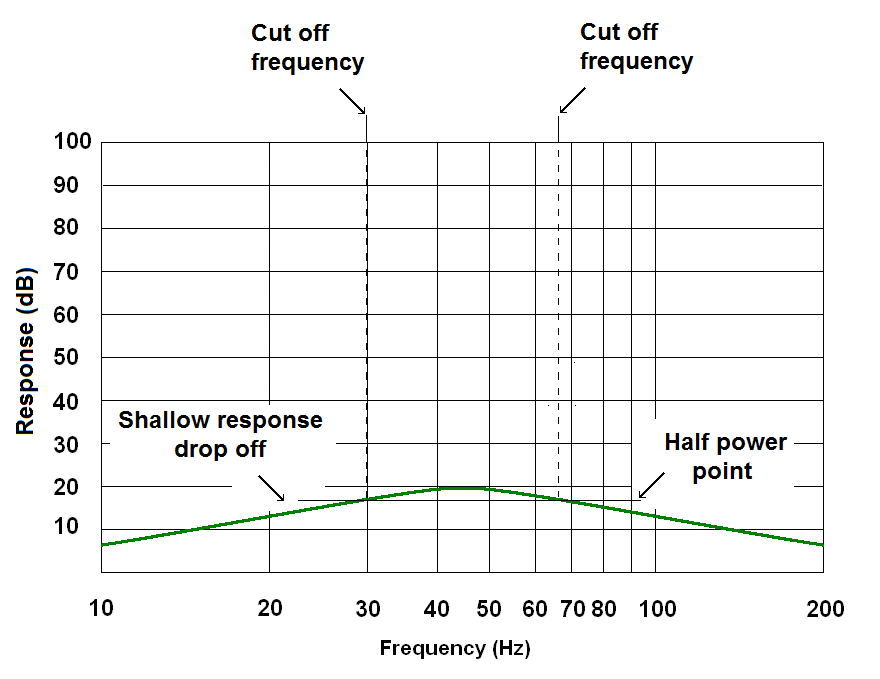
|
A low Q filter
The pass band of a low Q filter is wide. However, the drop off above and below the pass band is shallow; the response of the filter does not drop off as much as you go above and below the pass band. |
Low Q filters have an inherent problem. Without the seep skirts they don't reject unwanted frequencies very well. What do you do if you want the steep drop off of a high Q filter and the wide band of a low Q filter?
Filters can be designed that are essentially multiple filters in one unit as follows:
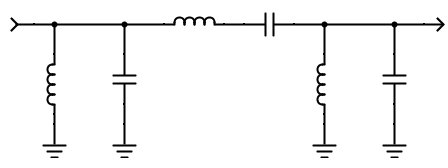
|
A Compound Filter
This is three bandpass filters in one. It is essentially two parallel bandpass filters with a series bandpass filter in between. |
The three stages in the above filter are tuned to slightly different frequencies. The first stage passes one range of frequencies while the middle stage passes another range that overlaps the first. The third state passes yet another range of frequencies.
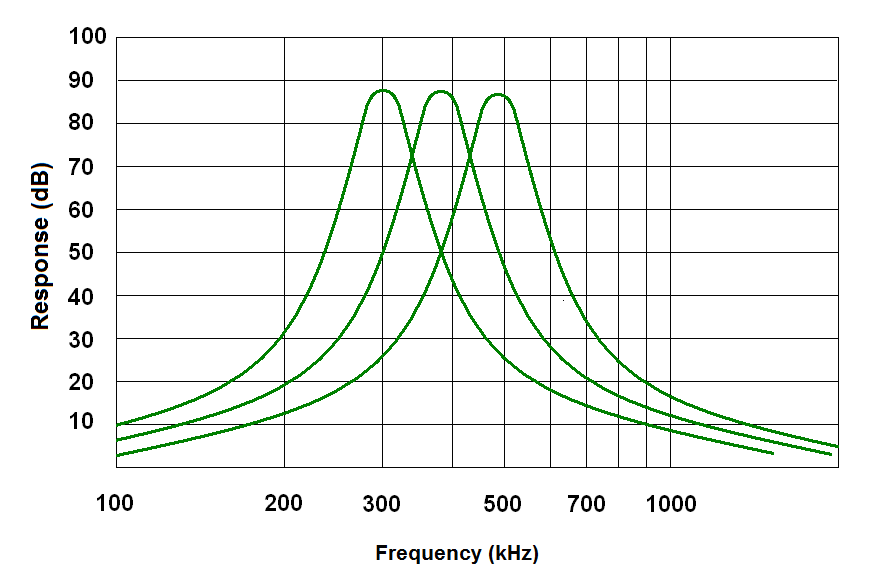
| Overlapping
Stage Responses |
The overall response of a compound filter is something like this.
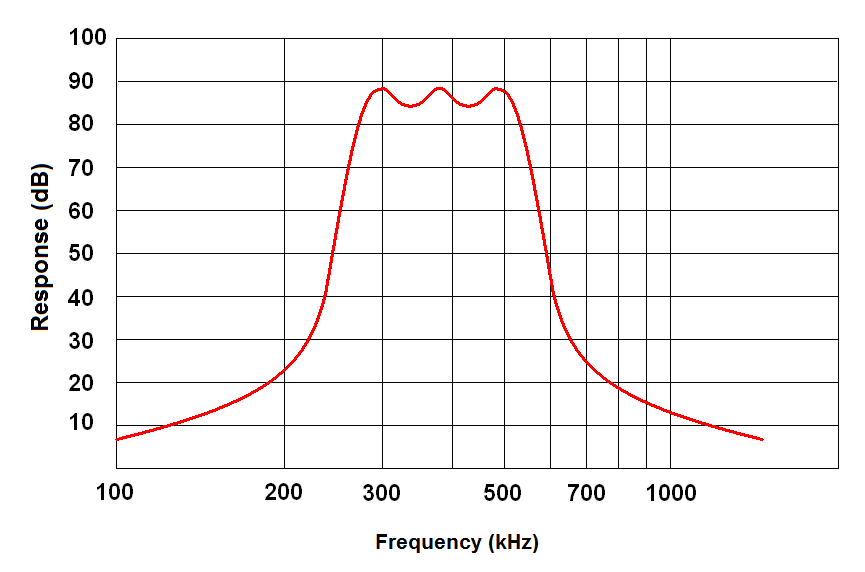
|
A Compound Filter's Overall
Response
The stages of a compound filter overlap to give an overall response something like this diagram |
There are several design types for compound filters. Some of these are the Chebychev filter, the Butterworth filter and the Constant K filter. Filters may also be made as part of the feedback loops of amplifiers. These are called active filters and have improved characteristics. Compound filter design is an engineering field and is beyond the scope of this course.
Electronic Filters
| Vocademy |