| Vocademy |
Kirchhoff’s voltage law
If there is a single resistor in a circuit, then all of the battery voltage will be seen across that one resistor. The following diagram shows the probes of a volt meter. The voltage that the meter will read is shown between the probes. If the probes are placed across the single resistor, the voltage will equal the battery voltage.
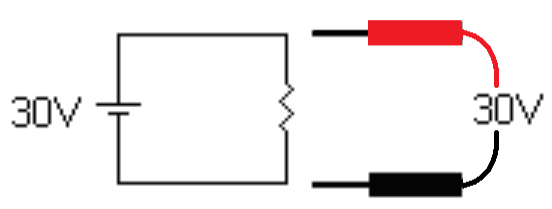
| With one resistor the entire battery voltage apperars across that resistor |
In the following circuit there are three resistors, 20, 30 and 10 ohms (60 ohms, total).
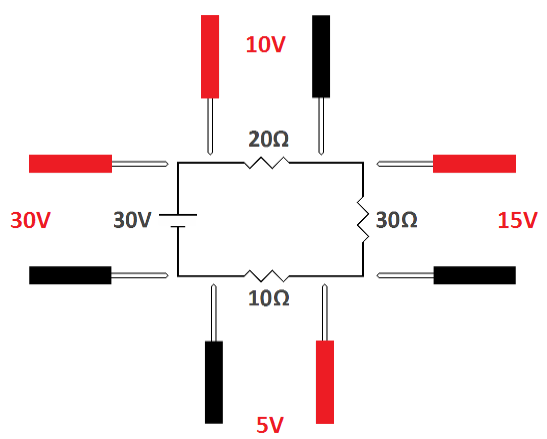
| The total voltage across the components in a series circuit adds up to the battery voltage. |
Let's change the resistors to a 50 ohm resistor, a 75 ohm resistor and a 25 ohm resistor.
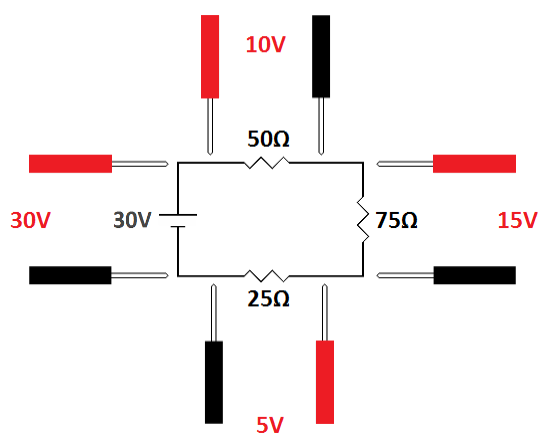
| The resistors are different but the proportions are the same. Therefore the voltages are the same. |
In the next circuit, the black probe of the volt meter is connected to the negative side of the battery and remains there. The red probe is moved to different points around the circuit to read the voltages at these points in relation to the negative side of the battery.
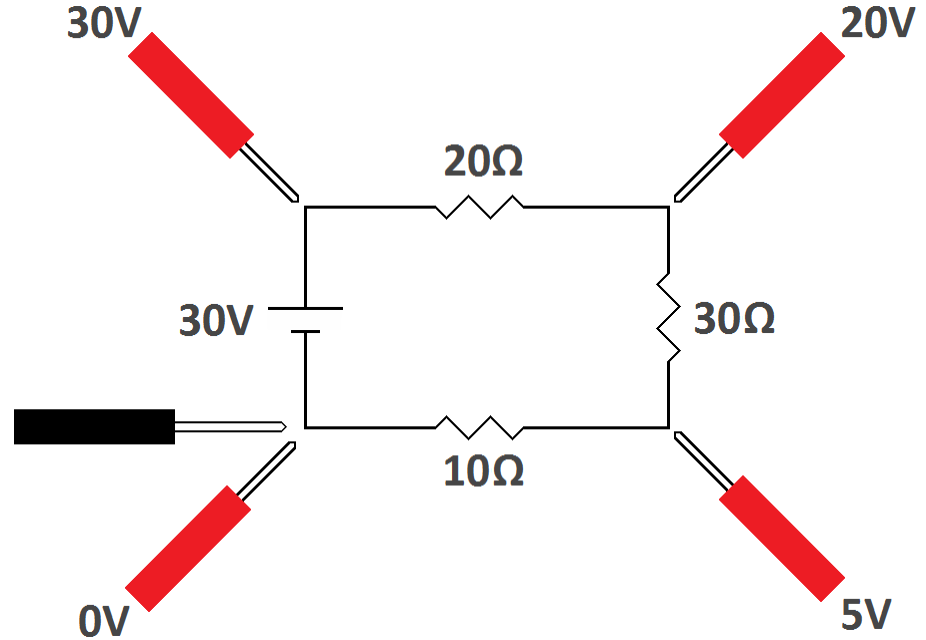
| Voltages referenced to the negative side of the battery |
Notice that when the red probe is
connected to the positive side of the battery, the meter reads 30
volts, which is the battery voltage. This makes perfect sense because
the meter is simply connected across the battery. When the red probe is
moved to the other side of the 20 ohm resistor it reads 20 volts. There
is a loss of 10 volts from the side of the resistor closest to the
battery compared to the side farthest from the battery. This voltage
drop, as it is called is the same 10 volts read when the meter probes
were placed across the resistor.
When the red probe is moved to the other side of the 30 ohm resistor the meter will read 5 volts. There is a loss of another 15 volts. This 15 volt drop is the same 15 volts read when the meter was placed directly across the 30 ohm resistor. Finally, there is a 5 volt loss across the 10 ohm resistor, leaving zero volts on the negative side of the battery. All of the voltage was lost in the process of going around the complete circuit. This is like walking downstream along a river. As you walk in the direction of flow you go lower and lower. Finally you reach the ocean which is as low as you can go. Remember that height, like voltage, is potential energy. As you walk downstream you go lower and lower losing potential energy. As you go around the circuit in the direction of conventional current flow you will have less and less voltage, finally reaching zero volts. This is a practical demonstration of Kirchhoff's Voltage Law. We start with the battery voltage, then subtract the voltage across each resistor, ending up with zero volts.
Notice that at the at the end of the circuit the red and black probes are both connected to the same place—the negative terminal of the battery. Remember that the voltmeter measures the voltage difference between the probes. If the probes are connected to the same point in the circuit there is no difference between them. The meter will read 0 volts telling you that there is no voltage difference between the probes. The meter does not read 0 volts because there is no voltage there. It is only telling you that both probes are at the same voltage.
The conventional expression of Kirchhoff's Voltage Law
Note that the above explains the conventional expression of Kirchhoff's Voltage Law—that the sum of the voltages in a series circuit equals zero. We added the battery voltage (30 volts) and then subtracted the voltage across each resistor (10, 15, and 5 volts), reaching zero volts after traversing around the circuit. The following diagram shows the conventional illustration of Kirchhoff's Voltage Law. Notice the voltage polarities—the orientation of the plus and minus symbols. The battery (the voltage source) is oriented with the positive side where conventional current exits the source. The resistors (power consumers) are oriented with the positive side where conventional current enters the component. This orientation mirrors Kirchhoff's Voltage Law's mathematics: voltage sources are positive, and power consumers are negative. We demonstrate Kirchhoff's Voltage Law by adding the magnitude of the voltage source and then subtracting the magnitudes of the power consumers. Here we have 30 - 10 -15 - 5 = 0.
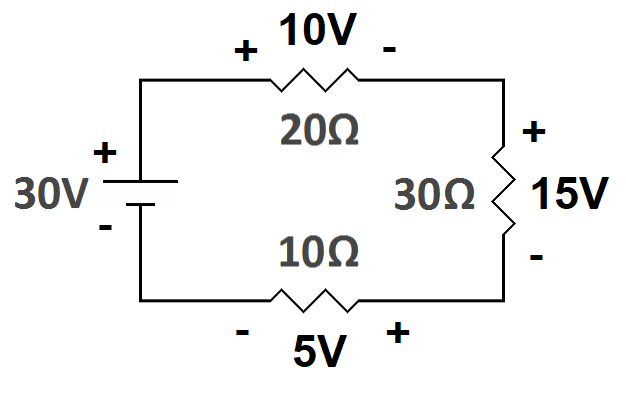 |
|
|
If there are multiple voltage sources, they are added to the equation. For example, let's say we reduce the battery voltage by five volts and add a 5-volt battery between the 20-ohm resistor and the 15-ohm resistor (this keeps the total voltage at 30 volts so we don't have to recalculate the current). The equation becomes 25 - 10 + 5 - 15 - 5 = 0.
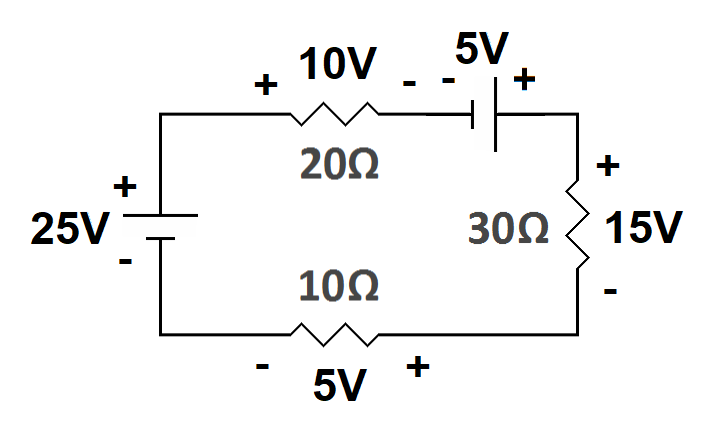 |
|
|
The orientation of the battery is arbitrary; we can orient the batteries any way we want to. However, the orientation of the resistor voltages depends on the current direction. Let's increase the first battery voltage to 30 volts and flip the orientation of the second battery (again, keeping the total voltage at 30 volts so we don't have to recalculate anything). Now, the voltage across the second battery is oriented the same as the voltages across the resistors—the second battery opposes the voltage of the first. In this case, we subtract the magnitude of the second battery, and the equation becomes 35 - 10 - 5 - 15 - 5 = 0.
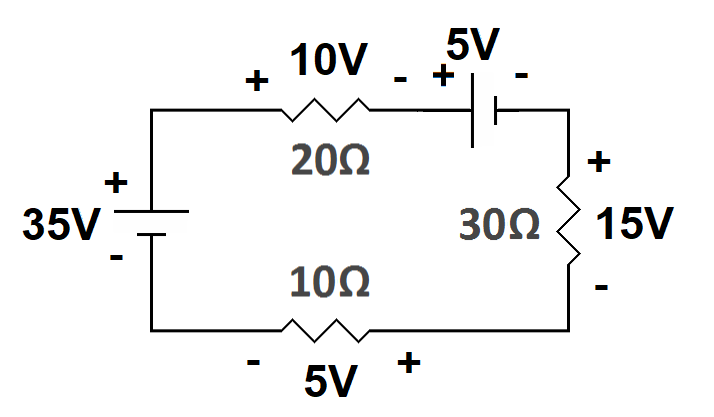 |
|
|
Notice that we still have the sum of the voltages across the resistors equaling the total voltage supplied by the batteries. We had to subtract one battery from the other since their orientations are reversed to find the total voltage (35 - 5 = 30). Nevertheless, Kirchhoff's Voltage Law works either way you look at it.
Unsticking some sticking points
Let's pause for a moment and make sure we understand this. This is a sticking point for many people. Repeating for emphasis, when you anchor the black probe at the negative side of a battery, then measure the voltages around the circuit with the red probe, you will get lower and lower voltages as you go from the positive terminal of the battery around the circuit. When the red probe reaches the negative side of the battery, it will read 0 volts. This is not because there is no voltage at this point. It is only because the red and black probes are at the same point in the circuit. The meter is telling you that there is no voltage difference between the probes, not that there is no voltage at that point. Don't forget that the voltmeter tells you the difference between two voltages, not an absolute voltage. Zero volts is not the absence of voltage. A voltmeter reads zero volts when both probes are at the same voltage. Think of the battery as a pump where electricity is sucked in the negative side and pushed out the positive side.
Another sticking point for some people is where current goes once it
reaches the negative side of the battery. Some people have no problem
with following the current around the loop, but wonder where it goes in
the end. Remember that the battery acts like a pump that circulates
electrical current around the circuit. It pushes conventional current
out the positive terminal and sucks it back in the negative side. The
current just goes round and round the circuit.[1]
A third sticking point was discussed previously in Ohm's Law and Thevenin's Theorem. Recall that you can't apply Ohm's Law to a power source unless you apply any resistance in that power source in series with the source of electromotive force. We used the common mistake new students make of attempting to apply Ohm's Law to a battery. In particular, we looked at a scenario of a 10-volt battery with a known internal resistance of one ohm. Then we asked why 10 amperes of current are not flowing through that one ohm of resistance. The answer is that the battery's internal resistance must be applied in series with the source of electromotive force. Therefore, as long as the battery's terminals remain unconnected, there is no path for current flow (review the battery model under output impedance under Thevenin's Theorem).
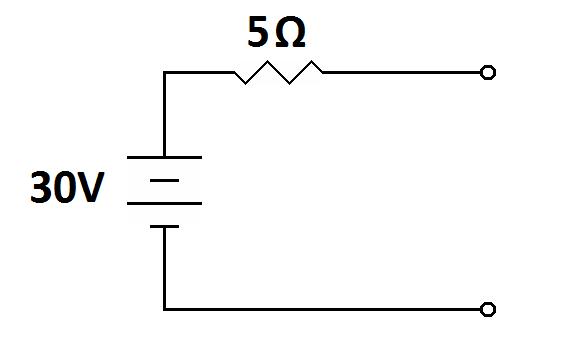 |
|
|
Let's replace the battery with the secondary of a transformer (to be discussed in AC circuits). The secondary of a transformer is a coil of wire embedded in a changing magnetic field and thus is a source of AC electromotive force. Let's say that transformer secondary is producing 10 volts (being AC volts is irrelevant at this point). Let's say the wire making up that transformer secondary consists of a superconducting material and thus has zero ohms of resistance. Essentially, we have a 10-volt battery (AC notwithstanding) with an internal resistance of zero ohms. Now, let's apply Ohm's Law to that transformer secondary. With 10 volts and zero ohms there must be infinite current flowing in that transformer secondary. Hopefully, you caught our mistake. We cannot apply Ohm's law to a power source unless any internal resistance in that power source is applied in series with the source of electromotive force. Here's the Thevenin equivalent circuit of the transformer secondary with the internal resistance (output impedance) of zero ohms correctly applied.
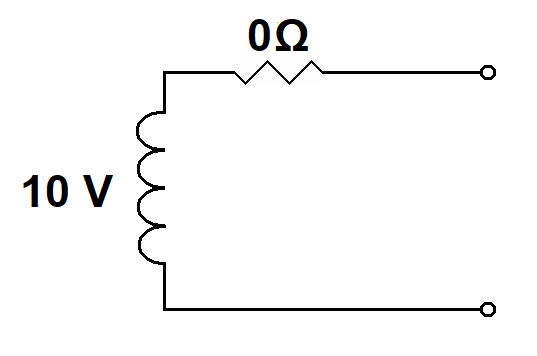 |
|
|
As you can see, the zero ohms of internal resistance doesn't provide a path for current flow unless there is a circuit connected across the terminals of the secondary.
Misunderstanding this principle leads to the false assumption that, since the resistance of the secondary is zero ohms, there can be no voltage across the secondary; you can't have voltage across a short circuit. Therefore, the voltage measured across the secondary exists only in the voltmeter; there is no voltage across the transformer secondary. Of course, we know that there can indeed be voltage across the secondary because the zero resistance is in series with the voltage source, not across it. However, once you fall into the above trap, Kirchhoff's Voltage Law becomes problematic. Considere the following diagram.
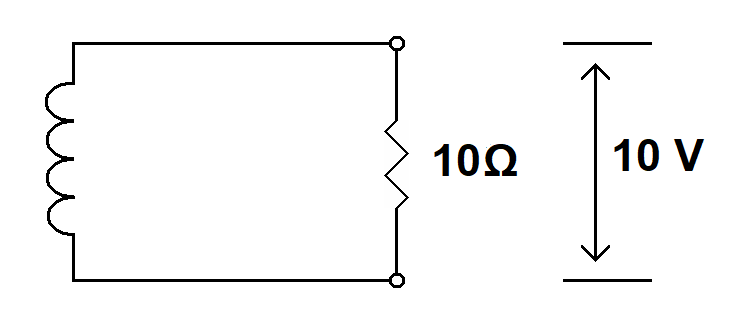 |
|
|
If there can be no voltage across the transformer secondary, due to it having zero ohms of resistance, voltage only exists across the 10-ohm resistor placed across the terminals of the secondary. This violates Kirchhoff's Voltage Law. There must be a voltage across the transformer secondary equal to the voltage across the resistor (of a polarity opposite to the voltage across the resistor, see the first diagram above). By misapplying Ohm's Law we find that Kirchhoff's Voltage Law fails. However, we know that there is indeed a voltage across the transformer secondary so Kirchhoff's Voltage Law works as expected.
Now you are armed with a correct understanding of how to apply Ohm's Law and Kirchhoff's Voltage Law sources of electromotive force.
Series Circuits and Kirchhoff's Voltage Law
—————————
| 1 | Of course, this isn't exactly what is really happening, but it sure looks like it is so let's move on. |
| Vocademy |