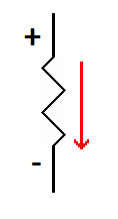
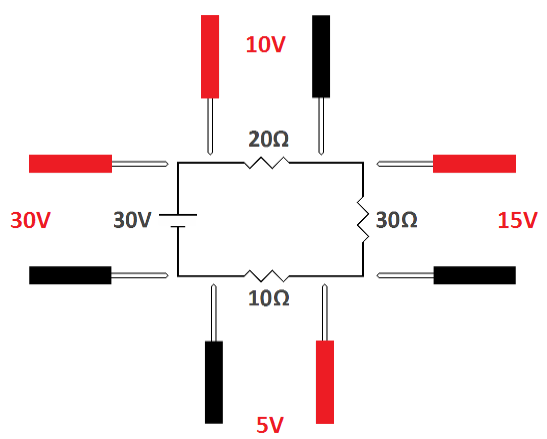
What voltage polarities should we expect in the circuit? If you look at
the circuit you will see that when measuring the voltage across the
resistors the red probe is placed nearest the positive terminal of the
battery. How do we know this is the correct orientation? When
conventional current enters a resistor there will be a back-up of
voltage behind that resistor. You will get a higher voltage where
conventional current enters the resistor and a lower voltage where the current exits the resistor.
The voltage will be positive where conventional current enters the
resistor and negative where it exits.
Remember that negative voltage is not
the opposite of positive voltage. A negative voltage is simply a
voltage that is lower than some other voltage (review
Polarity).
Likewise a positive voltage is a voltage that is higher than some other
voltage. Voltages are always considered by how they relate to other
voltages. In this example we have two isolated voltages. We are not
comparing them to voltages anywhere else in the circuit. We are only
interested in how the two voltages relate to each other. In this case
the higher voltage is considered positive and the lower voltage is
considered negative.
A current source, such as a battery is opposite.
Notice that the battery voltage is positive where the conventional
current exits and negative where the current enters. A battery
pushes current out the positive terminal so that is where the pressure
is higher. It sucks the current back in the negative terminal so that
is where the pressure is lower. With a resistor, electricity backs up
where the current enters causing an increase in voltage at that point. Ther is a
corresponding decrease where the current exits the resistor.
If you look at the diagrams for Kirchhoff's Voltage Law, you will see
that the polarity across the battery is opposite to the polarity across
the resistors.
| The polarity of the voltage across the battery is opposite to the voltage across the resistors. |
Now we can make sense out of the proper way to state Kirchhoff's
Voltage Law. Let's flip a coin and call the polarity across the battery
positive and the polarity across the resistors negative (it will work
just as well if we do it the other way around). That starts us out with
positive 30 volts. Now we add the negative voltages across the
resistors. Since adding a negative number is the same as subtracting a
positive number we are actually subtracting the voltages across the
resistors. Therefore, we start with 30 volts, subtract 10, subtract 15
then subtract 5 and we end up with 0 volts.
30 + (-10) + (-15) + (-5) = 0
or
30 – 10 – 15 – 5 = 0
We add all the voltages together and we get zero. There's Kirchhoff's Voltage Law.