| Vocademy |

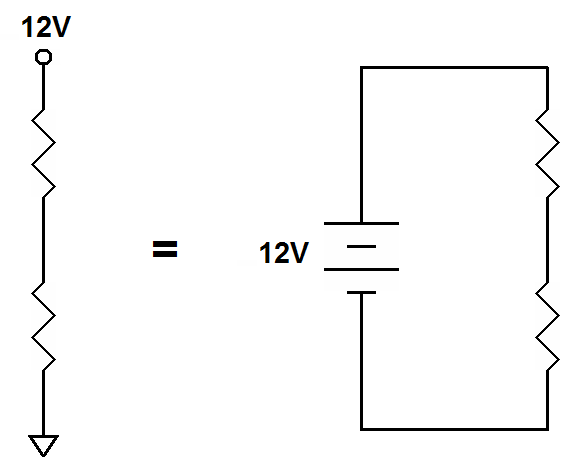
| The circuit to the left is the same as the circuit to the right. The
circle connects to the positive terminal of the 12 volt battery and the
ground symbol connects to the negative terminal. |
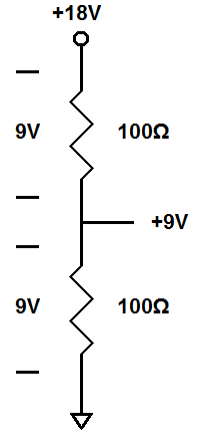
| Two equal resistors in series will have equal voltage. Measured compared to ground the voltage between two resistors will be ½ the total voltage (the line next to the “+9V” is just to show where the voltage is measured). |
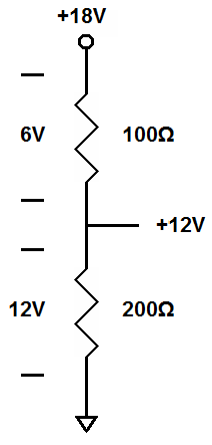
| If the resistors are not equal, the voltages change proportionally. They still add up to the total voltage. The voltage between the resistors, compared to ground, will be the voltage across the resistor connected to ground. Here the 200 ohm resistor is connected to ground. There are 12 volts across that resistor. Therefore, the voltage between the resistors is +12 volts. |
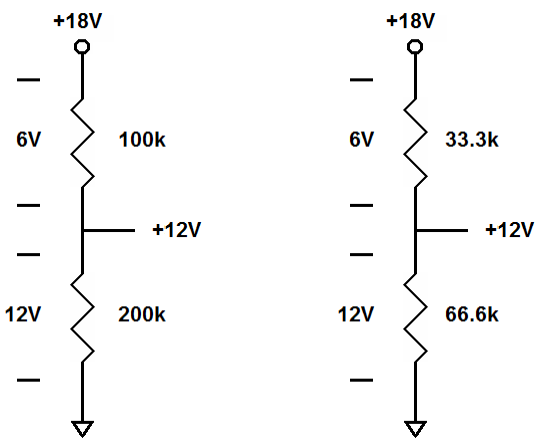
| It doesn't matter what the actual resistors are. As long as the proportions don't change, the voltages don't change. These voltage dividers have radically different resistors, but since the proportions are the same the voltages are the same. |
 3 = 6). That is the voltage across the lesser resistor, 6 volts here.
The greater resistor will have twice this value, 12 volts in this case.
3 = 6). That is the voltage across the lesser resistor, 6 volts here.
The greater resistor will have twice this value, 12 volts in this case.
| Vocademy |