| Vocademy |
Kirchhoff’s current law
The third fundamental law of
electronics is Kirchhoff’s Current Law. It states that the sum of the
currents flowing into a node will equal the sum of the currents flowing
out of that node. Like Kirchhoff's Voltage Law this may be a bit
confusing. Here's a more practical way to put it: In each branch of a
parallel circuit you will have a certain amount of current. If you add
all the currents in all the branches together you get the total
current. Therefore, the total current exits the battery, splits up
amung the several branches of the circuit then all comes back together
to be sucked back into the battery.
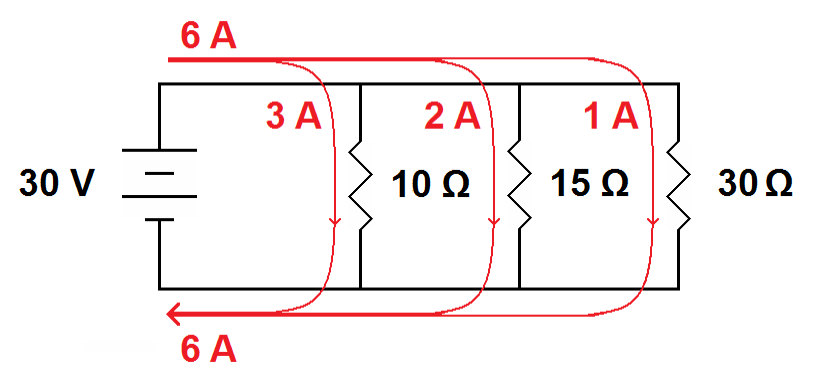
| Current flow through a parallel circuit. The total current of 6 amps splits into three branches (3 amps, 2 amps and 1 amp) then combines back into 6 amps to return to the battery. |
Imagine that you have the water running in the kitchen sink and the
bathtub. There are 30 gallons of water entering the house every hour.
20 of those gallons are going down the bathtub drain and 10 gallons are
going down the kitchen drain. What it the total amount of water going
down the sewer pipe? It is of course 30 gallons per hour. The same
amount of water entering the house. This is exactly what Kirchhoff's
Current Law states about electricity. It simply means that whatever
current leaves the battery returns to the battery, no matter how many
times it branches between. It all eventually comes back together and
returns to the battery.
Kirchhoff’s Current Law can be expressed by the following formula.
Kirchhoff’s Current Law can be expressed by the following formula.
IT = IR1 + IR2 + IR3 etc.
Where:
IT is Total current flowing through the parallel circuit.
IR1, IR2 and IR3 is the current flowing through each of the resistors in the circuit
IR1, IR2 and IR3 is the current flowing through each of the resistors in the circuit
Voltage in a parallel circuit
Parallel circuits have the same voltage across each resistor. Each resistor is connected directly across the battery so the entire battery voltage is across each resistor.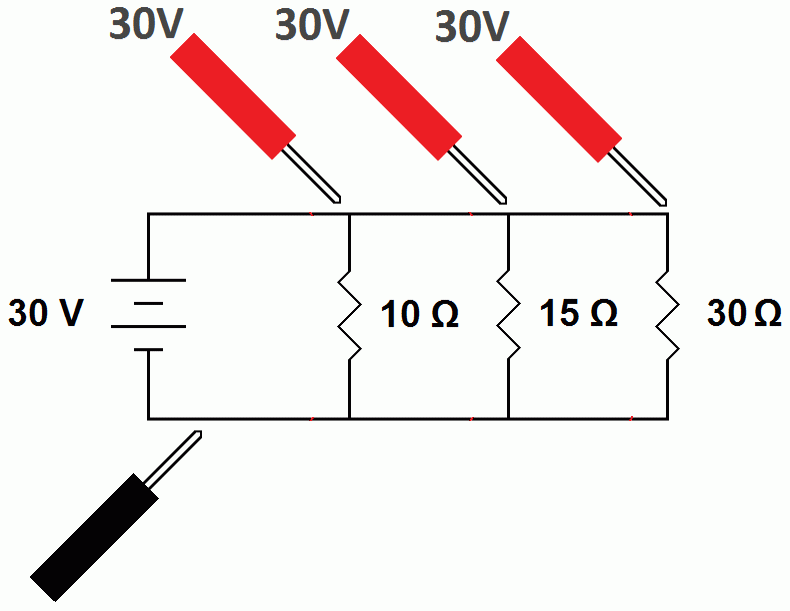
| The voltage is the same across all the resistors in a parallel circuit. These voltages do not add together. We do not have 90 volts in this circuit, just 30. |
The voltages across the resistors do not add together. If you have 30 volts across three resistors in parallel, it is the same 30 volts across each resistor for a total of 30 volts, the voltages do not add together to become 90 volts In the above example 30 volts across 10 ohms results in 3 amperes, 30 volts across 15 ohms results in 2 amperes and 30 volts across 30 ohms results in 1 ampere. This adds up to 6 amperes, the total current. Notice that 6 amperes leave the battery, it divides into 3 amperes, 2 amperes and 1 ampere, then all three currents recombine into the original 6 amperes to return to the battery.
Exercises:1
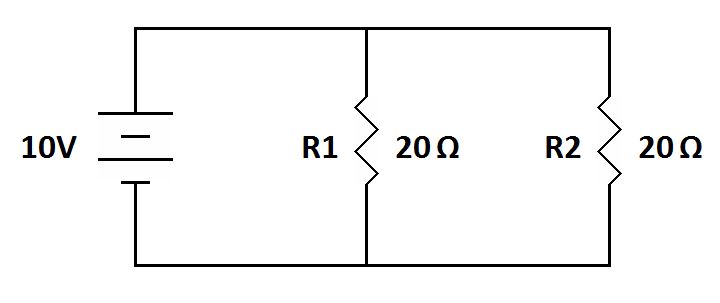 |
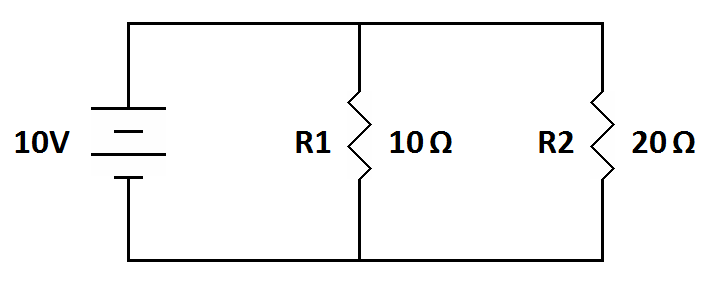 |
| 1) What is the voltage across R1? ________ What is the voltage across R2? ________ What is the current through R1? ________ What is the current through R2? ________ What is the total resistance in the circuit? ________ What is the total current in the circuit? ________ |
2) What is the voltage across R1? ________ What is the voltage across R2? ________ What is the current through R1? ________ What is the current through R2? ________ What is the total resistance in the circuit? ________ What is the total current in the circuit? ________ |
Summary:
In a parallel circuit (more than one path for current to follow):
- The total resistance is calculated by the following formula:
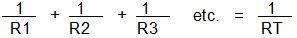
- The total current is the sum of the currents through each resistor (Kirchhoff's current law).
- This current is distributed proportionally among the resistors. For example, if one resistor is twice the value of another resistor in the same parallel circuit, it will have half the current flowing through it. If two resistors are equal, the current passing through them will be equal.
- The voltage is the same across each resistor.
| 1 |
1) 2) |
The
voltage is the same everywhere, so R1 and R2 have 10 volts each, The
resistors are the same so the currents are the same at 0.5 amps (500mA)
each. The total resistance is 10 ohms and the total current is the sum
of the currents through both resistors, which is 1 amp. Both resistors have 10 volts across them. The current through R1 is 1 amp and the current through R2 is 0.5 amps (500mA). The total resistance is 6.66 ohms and the total current is 1.5 amps. |
Parallel Circuits and Kirchhoff's Current Law
Parallel Circuit Exercises
| Vocademy |