| Vocademy |
Impedance matching
Since a circuit with a low input impedance requires a relatively high current, a circuit with a low output impedance is required to drive it. A low output impedance goes with a low input impedance.
A circuit with a low output impedance can generally deliver a wide range of current. Therefore, there is usually no problem driving a circuit that has a high input impedance with a circuit that has a low output impedance.[1]
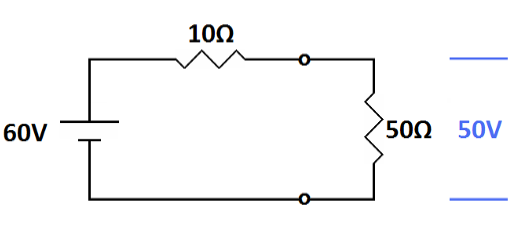
| The output impedance (Z out) is low (10 ohms) and the input impedance
(Z in) is high (50 ohms). Most of the available voltage is developed
across the input impedance. This is generally a good thing. |
The most problematic situation is when a high output impedance is coupled to a low input impedance. The low input impedance will probably demand so much current that there is too much voltage lost across the high output impedance.
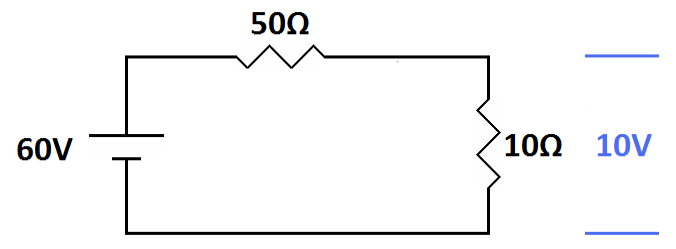
| The output impedance is high (50 ohms) and the input impedance is low (10 ohms). Only 1/6 of the available output voltage is developed across the input impedance. This impedance mismatch is generally undesirable. |
Power delivery
When the goal is to transfer the maximum amount of power from one circuit to another, the input impedance should be the same as the output impedance. The following illustration shows how the maximum power is transferred from one circuit to another when the input impedance matches the output impedance.
| Impedance matching and power delivery |
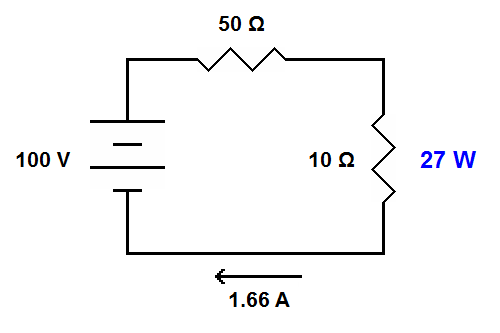 |
| The 50 ohm resistor represents the output impedance of one circuit. The 10 ohm resistor represents the input impedance of the next circuit. In this example the output impedance is five times the input impedance. Here the power delivered to the input is 27 watts (you can confirm this with the formula: P=I2R). |
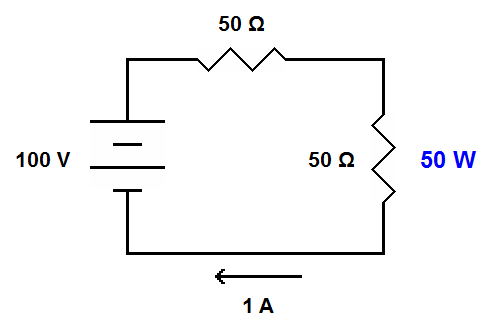 |
| When the input impedance is increased to match the output impedance, the power delivered to the input is at its greatest. In this example it is 50 watts. |
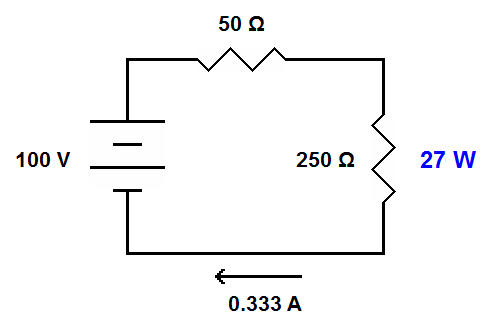 |
| When the input impedance exceeds the output impedance less power is delivered to the input impedance. In this example the input impedance is five times the output impedance. As in the first case the power delivered to the input is 27 watts. |
In the first case above (a 50 ohm output impedance driving a 10 ohm input impedance), the power dissipated by the output impedance is 138 watts (1.66 amps squared times 50 ohms). This demonstrates how an impedance mismatch can damage circuits. Let's assume the equipment is a radio transmitter designed to work with an antenna that has a 50 ohm impedance. If the antenna has an impedance of 10 ohms the output impedance of the transmitter will have to dissipate 138 watts. It was designed to dissipate only 50 watts. This impedance mismatch will likely damage the transmitter.
The basic rule is:
Matching a power supply to its load
Let's say you have a radio that runs on batteries or from an AC adapter. You can't find the adapter that came with the radio, but the electrical rating sticker says it runs on 12 volts at 1 amp. You have a spare AC adaptor that is rated at 12 volts and 2 amps. Can you use this adapter with the radio or will the 2 amps fry it?Go for it. In fact, if it was rated at 12 volts and 1,000 amps it would be no problem. How can that be? The 2 amp rating of the AC adapter is its maximum rating. The load will only take the current it needs. It will happily take the 1 amp it needs and leave the rest. According to Ohm's law, the current is determined by the voltage divided by the impedance. What is the impedance of the radio? We can use Ohm's law to figure that out. The rating sticker says 12 volts at 1 amp. Sounds like an Ohm's law problem to me. 12 volts ÷ 1 amp = 12 ohms. This radio, when turned up to full volume, blasting the maximum power out its speakers will have an impedance of 12 ohms. Put our 12-volt AC adapter on that radio and that radio will take 1 amp from the adapter. The rest of the 2-amp rating is extra reserve capacity. We could power another 1-amp radio, or whatever at the same time.
So, what does the 2-amp rating of the adapter tell us? It tell us that the adapter can deliver a maximum of 2 amps. We can power our 1-amp radio and something else, up to another 1 amp for a total of 2 amps. If you try to exceed 2 amps the voltage will start to drop. The more current current we take above the maximum rating, the lower the output voltage goes.
What about an AC adapter rated at 24 volts and 1 amp. Will that work? Let's calculate that. Our radio at full volume is 12 ohms, that's 24 volts ÷ 12 ohms = 2 amps. Well, that adapter isn't going to give us 2 amps. It's only rated at 1 amp. However, unless it has specific current-limiting circuitry to prevent it from delivering more than one amp, it will give you something more than the 1 amp it is rated for. So, you might get away with it, but you are in danger of damaging the AC adapter, the radio or both.
The bottom line is, when matching a voltage source, such as an AC adapter or other power supply to a a load, you want the current rating of the source to meet or exceed the current rating of the device it is delivering power to. It doesn't matter how much it exceeds the demand. However, the voltage of the power supply, must usually match the voltage rating of the load[2]. In our case, with a radio rated at 12 volts and 1 amp, we want an adapter with a voltage rating of 12 volts and a current rating of 1 amp or more
Thevenin's Theorem, Output Impedance and Input Impedance
Choosing a Plug-in Power Supply
| Vocademy |
