Understanding Ohm's law and Kirchhoff's laws is essential to analyzing
any electronic circuit. Let's take this first of several opportunities
to practice Ohm's law and Kirchhoff's laws to be sure we thoroughly
understand them.
In the following circuit, TP1 and TP2 are test points where we measure
voltage. Part of this exercise is to calculate the expected voltages at
these points. We will make the typical assumption that the designated
ground is the negative terminal of the battery. That is where the black
probe of the imaginary volt meter will be placed. The other unknowns
are the values of R1 and R3. Take all the time you need to solve this
puzzle before reading the solution.
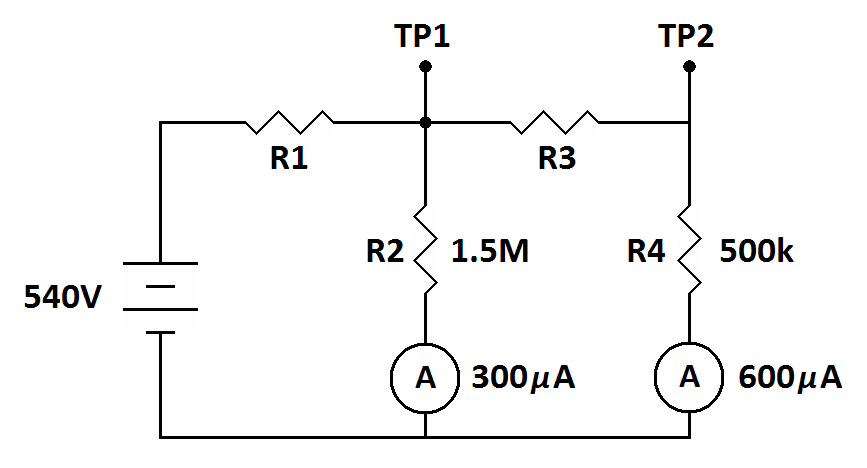
Find:
R1 ____ Ω
R3 ____ Ω
TP1 ____ V
TP2 ____ V
Solution:
First look for components where you already have enough information to
use Ohm's law to calculate everything about that component. Let's start
with R2.
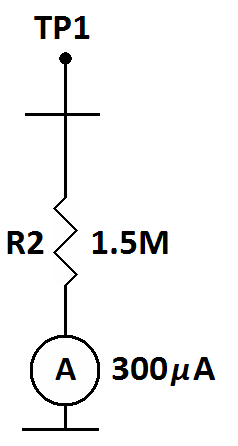
R2 has a value of 1.5 megaohms and has 300 microamps of current flowing
through it. With this we can calculate the voltage across it. Get your
calculator and follow along. We have 1.5 Mega-something, so we move the
decimal point six places to the right for 1,500,000. This gives us the
resistance in ohms. We also have 300 micro-something, so we move the
decimal point six places to the left for 0.000,3. This gives us the
current in amps. We don't know the voltage so we multiply the current
by the resistance. On the calculator that is...
1
5
0
0
0
0
0
X
.
0
0
0
3
=
450
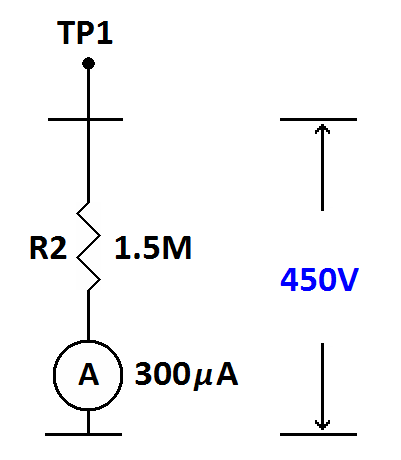
That will be 450 volts. Since the bottom of R2 is connected to ground
(the current meter is essentially a short circuit so there is no
voltage across it) and the voltage at TP1 is measured in relation to
ground. The voltage across R2 determines the voltage at TP1, which is
450V.
Now let's do the same thing for R4.
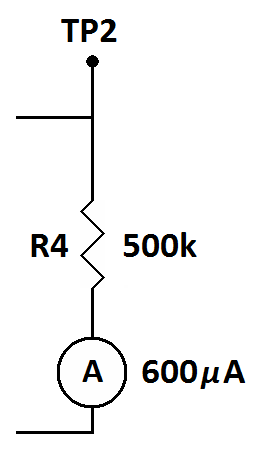
R4 has a value of 500 kiloohms and has 600 microamps of current flowing
through it. We have 500 kilo-something, so we move the decimal point
three places to the right for 500,000 ohms. We also have 600
micro-something, so we move the decimal point six places to the left
for 0.000,6 amps. Now we multiply again. On the calculator that is...
5
0
0
0
0
0
X
.
0
0
0
6
=
300
Giving 300 volts. Again,
R4 is connected to ground so the voltage across it is also the voltage
at TP2, which is 300V.
Now we know the voltages at both TP1 and TP2.
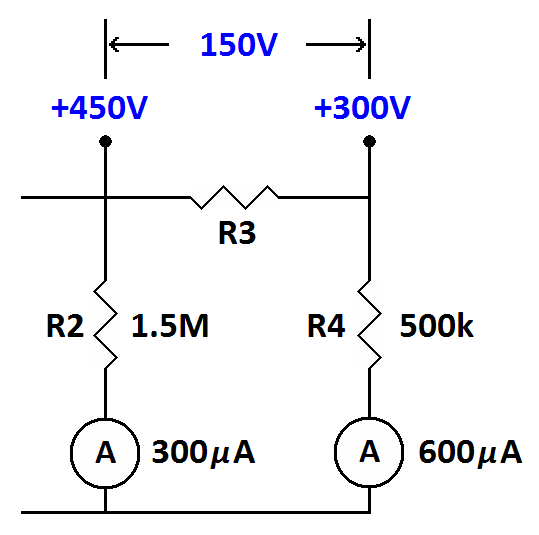
Since voltage is always a difference we now know the voltage across R3.
If only we knew the current through R3 we could calculate its value.
Actually, we do know the current through R3. R3 and R4 are in series
with each other (only one current path). Whatever current goes through
R4 must first go through R3 (so to speak). Therefore, R3 has 150 volts
across it and 600 microamps of current going through it. Let's
calculate its value. We know the voltage so we divide into it...
1
5
0
.
0
0
0
6
=
250000
Move the decimal point
three places to the left and that makes R3 250 k.
Now let's tackle R1
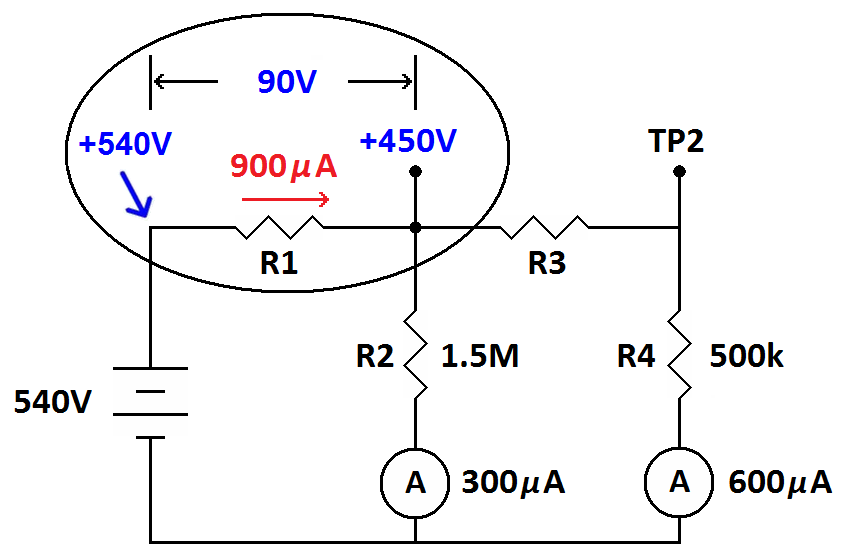
We start out with 540 volts and end up with 450 volts after passing R1.
There is a drop of 90 volts across R1. Now all we need is the current
through R1 to calculate its value. After R1 the circuit changes from a
series circuit to a parallel circuit. Kirchhoff's current law says that
the currents in the two legs of the parallel circuit must add up to the
total current that started from the battery. This means that R1 must
have 900 microamps flowing through it. Now we just divide that into the
90 volts across it and we have its value. On the calculator that is...
9
0
.
0
0
0
9
=
100000
R1 has a value of
100,000 ohms. Move the decimal point three places to the left and we
have 100k.
