| Vocademy |
Capacitors

Various capacitors
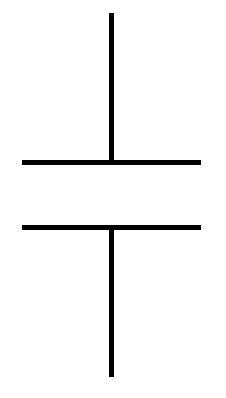
Schematic symbols
 |
 |
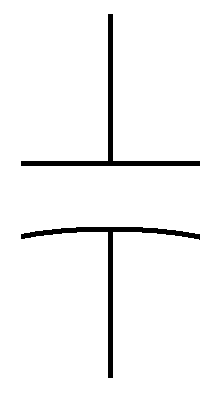 |
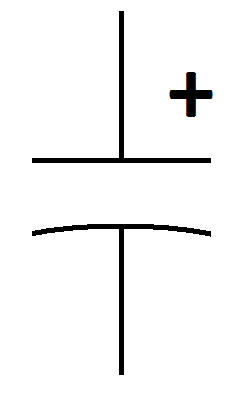 |
| Non-polarized | Polarized |
| The symbol on the lower left is often used to distinguish a polarized
capacitor (with the straight line representing the positive plate), but
this is not always the case. |
What is capacitance
Capacitance is the ability to store energy as a volume of electricity under electrical pressure[1]. A capacitor acts much like a compressed air tank for electricity. If you force air into a compressed air tank, you will get some air pressure in the tank. If you force more air into the tank you will get more pressure. Force more air in you get yet more pressure. You can continue this until one of two things happens: either there is so much pressure in the tank that you can't push any more air into it (the tank pressure is equal to whatever pressure you can apply to the air you are trying to force into it) or the tank ruptures and is destroyed.A capacitor acts much the same way. If you force electricity into a capacitor you will get some voltage across its terminals. If you push more electricity into the capacitor, you will get more voltage. If you push more in you will get yet more voltage. You can continue this until one of two things happens: either the voltage across the capacitor is so high that you can't push any more electricity into it (the capacitor voltage has reached whatever voltage you have to force electricity into it) or the insulation inside the capacitor fails and the capacitor is destroyed.
The farad
Capacitance is measured in units called farads. By definition, if you
force one coulomb of charge (approximately 6,241,509,480,000,000,000
electrons) into a capacitor, and after that, the capacitor has 1 volt
of potential across its electrodes, that capacitor has a capacitance of
1 farad. Until fairly recently, capacitors with high values tended to
be physically large and expensive. A traditional one-farad capacitor
may be as large as a liter bottle. Therefore, typical capacitors tend
to have low values. Capacitors labeled in the microfarad (μF)
or even the picofarad (pF) range. A capacitor with a value in the
millifarad range will usually be labeled in thousands of microfarads. A
capacitor in the nanofarad range will usually be labeled in thousands
of picofarads. It is rare to see capacitors labeled in the millifarad
or nanofarad range. (see Units of Measure above).
| Capacitor value |
Typical label |
| 0.001 farad (1 millifarad) |
1000 μF |
| 0.47 farad (470 millifarads) |
470000 μF |
| 0.000001 farad (1 nanofarad) |
1000 pF |
| 0.000033 farad (33 nanofarads) |
33000 pF |
Today, new technologies, such as the electric double-layer effect, can
be used to make high value capacitors in a very small size. One example
is a 1 farad, 2.5V aerogel capacitor that is 7/16 inch long and 5/16
inch in diameter and sells for about $5.00.
Sometimes, especially in material published before the mid 1960s, capacitors in the picofarad range are specified in micro-microfarads (μμF). A micro-microfarad is the same as a picofarad.
Sometimes, especially in material published before the mid 1960s, capacitors in the picofarad range are specified in micro-microfarads (μμF). A micro-microfarad is the same as a picofarad.
Reading capacitor values
Large capacitors are usually clearly marked with their capacitance in microfarads. Usually, the Greek letter mu (μ)
is used to represent the micro in microfarads. However, sometimes the
modern letter U is used. Therefore, a 10,000 microfarad capacitor may
be marked 10,000UF.
Confusion Alert!
Confusion Alert!
Many capacitors may be labeled with
“mF” (lower case “m”). In this case "mF" means microfarads, not
millifarads. This is supposedly because the labeling equipment owned by
the manufacturers is not capable of printing the Greek letter mu (μ).
Capacitors are also commonly labeled with “MF” (upper case “M”). These
are not megafarads. They are still microfarads.
1000MF 1000mF 1000μF
All these labels represent 1,000 microfarads
All these labels represent 1,000 microfarads
With smaller capacitors, particularly ceramic capacitors the
capacitance is labeled as nothing more than a number printed on the
capacitor. If this number is a whole number, the value is in
picofarads. If the value is a decimal fraction, the value is in
microfarads. Therefore, a ceramic capacitor labeled ".47" has a value
of 0.47 microfarads. A ceramic capacitor labeled "47" has a value of 47
picofarads.
If the number on a ceramic capacitor has three digits, the capacitance is decoded much like the resistor code with the capacitance in picofarads. The first two numbers are the significant digits and the third number is the number of zeros to put after them. Therefore, a capacitor labeled 103 would be have a value of 10,000 picofarads, which is the same as .01 microfarads. A ceramic capacitor labeled 103 and one labeled .01 have the same capacitance.
A letter after the number on a ceramic capacitor represents the tolerance, the percentage that the actual value may differ from the printed value. The tolerance values are: J=5%, K=10% and M=20%.
If the number on a ceramic capacitor has three digits, the capacitance is decoded much like the resistor code with the capacitance in picofarads. The first two numbers are the significant digits and the third number is the number of zeros to put after them. Therefore, a capacitor labeled 103 would be have a value of 10,000 picofarads, which is the same as .01 microfarads. A ceramic capacitor labeled 103 and one labeled .01 have the same capacitance.
A letter after the number on a ceramic capacitor represents the tolerance, the percentage that the actual value may differ from the printed value. The tolerance values are: J=5%, K=10% and M=20%.
| .47 |
= |
0.47 microfarads (470,000 picofarads) |
| .047 |
= |
0.047 microfarads (47,000 picofarads) |
| 47 |
= |
47 picorarads |
| 473 |
= |
47,000 picorarads |
| Various capacitor labels and their meanings. Notice that both ,047 and 473 mean 47,000 picofarads. |
Capacitor voltage ratings
As stated above, if you put too much voltage across a capacitor, the insulation will break down, destroying the capacitor. Certain types of capacitors will explode if too much voltage is applied to them. The voltage printed on a capacitor is its voltage rating, which should not be exceeded.Factors affecting capacitance
Any time you have two conductors separated by an insulator you have a capacitor. Pick up any two pieces of metal and hold them up, making sure they are not touching. This is two conductors (metal) separated by an insulator (air). Is this a capacitor? You betcha.
| A capacitance demonstrator consisting of two parallel plates of metal separated by air. |
Capacitance is primarily determined by the area of the conducting surfaces and their distance from each other. If you increase the size (area) of the conductors you will have more capacitance. If you increase the distance between the conductors you will have less capacitance. Therefore, if you want a lot of capacitance you need conductors with a lot of surface area very close to each other.
If enough voltage is placed across a capacitor the insulating material will break down. This typically causes permanent damage in the form of a short circuit (usually accompanied by an explosion). Generally, the more distance between the conductors, the more voltage the capacitor can handle. Higher voltage capacitors tend to be larger than lower voltage capacitors.
Capacitors Part 1 - Introduction
| Vocademy |