Resistance with capacitors

With a compressed air system, if there is a restriction in the pipe leading to the storage tank, the airflow to the tank will be impeded and the tank will take longer to fill. Likewise, if a resistor is placed between a capacitor and the voltage source it will take longer for the capacitor to charge than if the resistor weren't there. Therefore, the time it takes a capacitor to charge is a product not only of the capacitance but also of any resistance in the circuit.

RC time constants

When a capacitor is charging it acts like an air tank that is being filled with compressed air. When you first connect an air compressor to an air tank, the tank starts to fill quickly. Over time the tank fills more slowly. This is because at first there is no pressure in the tank to resist the inflow of air. Over time the tank builds pressure which pushes back on the incoming air. As the pressure in the tank approaches the pressure of the compressor the tank fills very slowly. Finally, there is so much pressure in the tank that the compressor cannot force any more air into it. This happens when the pressure in the tank equals the maximum pressure of the compressor. This is quite noticeable when you fill your tires with an air compressor that has barely more pressure than the tires. Toward the end the air goes into the tire very slowly.

A charging capacitor acts the same way. When you first connect a battery to a capacitor the capacitor charges quickly as the electricity rushes into the empty capacitor. Over time the capacitor charges more slowly as the voltage in the capacitor increases and pushes back on the incoming electricity. When the voltage in the capacitor approaches the voltage of the battery the capacitor charges very slowly. Finally the battery cannot force any more electricity into the capacitor. This happens when the voltage in the capacitor equals the voltage of the battery.

If you restrict the flow of air into a storage tank, it will take longer to fill. Likewise, if you restrict the flow of electricity into a capacitor, it will take longer to charge. Also, a larger tank will take longer to fill than a smaller tank, just as a capacitor with more capacitance will take longer to charge than a capacitor with less capacitance.
Let's make an imaginary demonstration circuit to watch a capacitor as it charges.

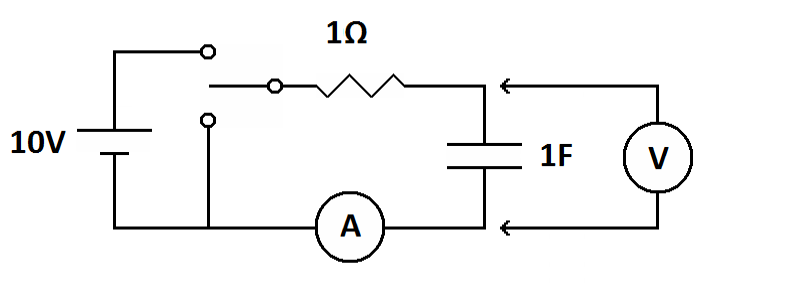
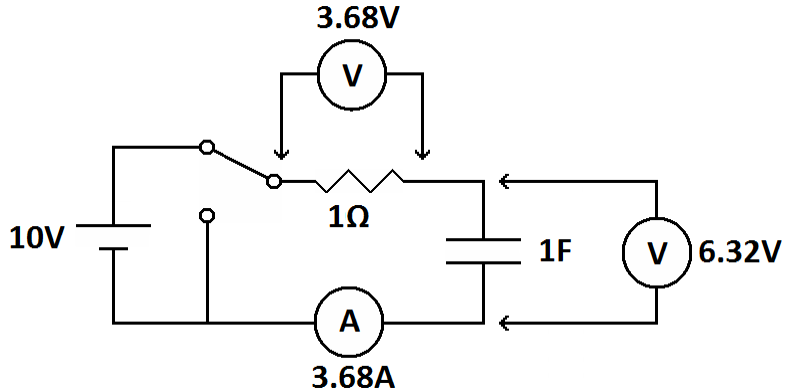
Demonstration circuit		Graph to show voltage and current over time

The above circuit consists of a 1 ohm resistor, a 1 farad capacitor and a 10 volt battery connected in series. The SPDT switch can be placed in two positions. In the up position you have a series circuit going from the positive terminal of the battery to the resistor, then to the capacitor and back to the negative terminal of the battery. This circuit will charge the capacitor. The down position takes the battery out of the circuit leaving a series circuit with just a resistor and a capacitor. The current meter and volt meter show that the voltage is being measured across the capacitor and the current is the total current in the series circuit. This circuit will discharge the capacitor.

First lets flip the switch to the discharge position to make sure the capacitor is completely discharged. We don't want any residual voltage skewing the demonstration.

First, discharge the capacitor

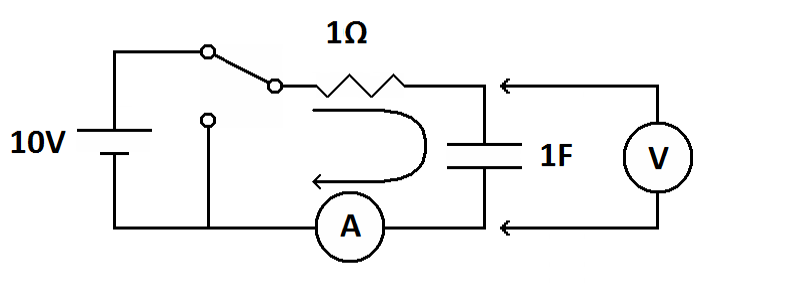
Now flip the switch to the charge position. Let's freeze time and look at what happens at that moment.

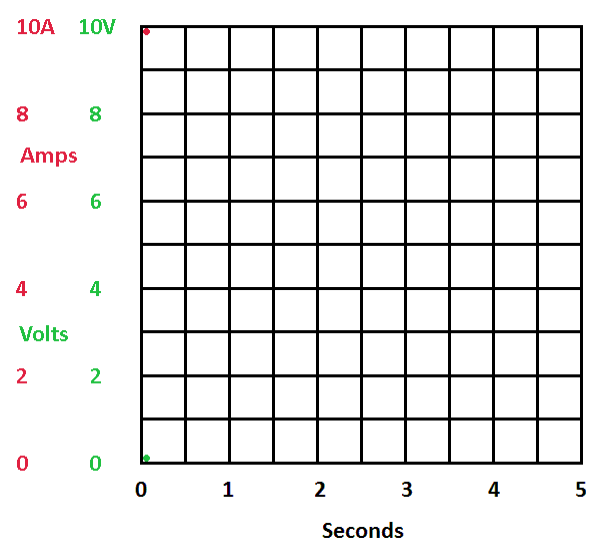The moment the switch is moved to the charge position the capacitor looks like a short circuit.		The voltage is zero (green dot in lower-left corner) and the current is at maximum (red dot in upper-left corner,10 amps in this case).

At the moment you close the switch the capacitor is empty so it offers no resistance to the inflow of electricity. The capacitor looks like a short circuit. How can this be? Electrons are streaming onto one plate of the capacitor. Since electrons repel each other these electrons push free electrons off the opposite plate. For every electron that enters the negative side of the capacitor an electron leaves the positive side. Electrons go in one side and out the other. Even though the electrons leaving the capacitor are not the same electrons that are entering the capacitor it looks like electrons are flowing through the capacitor.

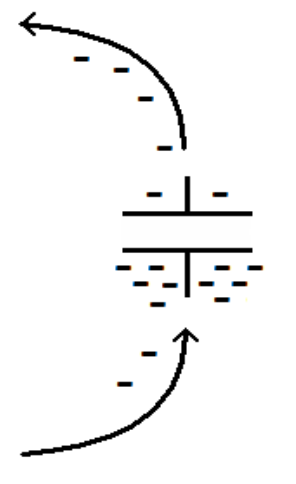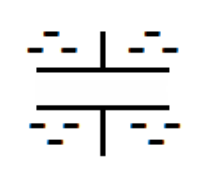
Discharged capacitor. The dashes represent free electrons on the plates. The two plates have an equal number of free electrons.		Charging capacitor. Electrons enter the negative electrode and leave the positive electrode. Current appears to flow through the capacitor (showing electron flow here because we are following the electrons).[1]

Again, the capacitor looks like a short circuit. How much voltage can you have across a short circuit? None. The voltage across the capacitor is zero. How much current is flowing. With the capacitor acting like a short circuit all that is left is a 10 volt battery and a 1 ohm resistor in series. The current is 10 amperes.

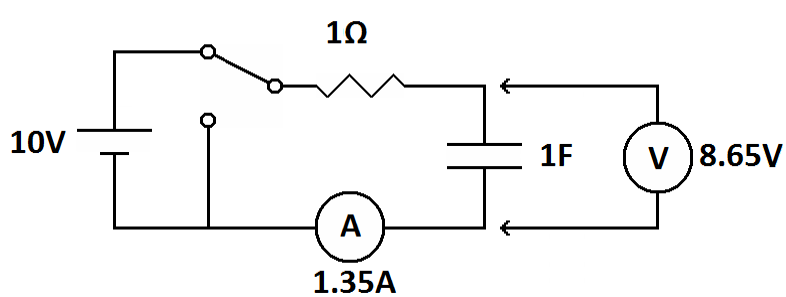
Now let's move time forward. Electrons will stream onto the negative plate and stream off the positive plate.  This causes a backup of voltage across the capacitor and it will begin to impede the inflow of electrical current. As a filling air tank will begin to push back on the air flowing into it, the capacitor begins to push back on the electricity flowing into it. Let's freeze time again after the capacitor has charged for one second.

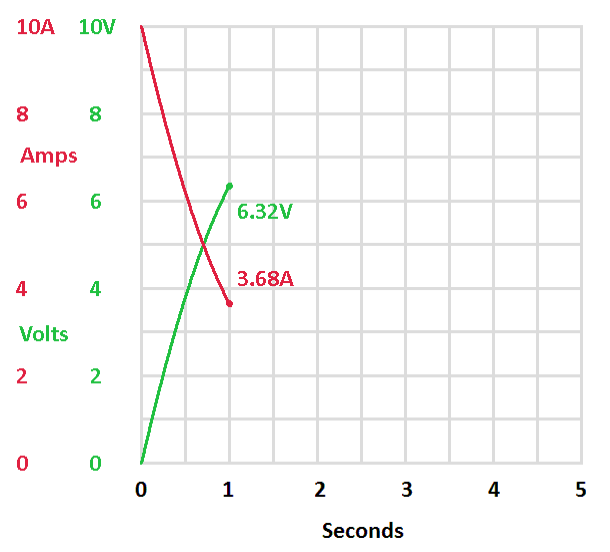After one second the capacitor has charged to 6.32 volts (63.2% of the battery voltage) and the current has decreased to 3.68 amps (36.8% of the maximum current or 10 amps minus 6.32 amps). The voltage has increased by 63.2% and the current has decreased by 63.2%

A capacitor time constant (RC time constant), by definition is the time it takes for a capacitor to charge to 63.2% of the source voltage (battery voltage). It is calculated by multiplying the resistance by the capacitance. In the following formula the lower-case Greek letter tau (t) represents the time constant.


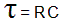
Where:

	τ	=	Time constant in seconds (the time it takes to reach 63.2% of the source voltage).
	R	=	Resistance in ohms
	C	=	Capacitance in farads

With a one ohm resistor and a one farad capacitor we have a time constant of 1 second (1 X 1 = 1). Therefore it will take one second for the capacitor to reach 63.2% of the battery voltage. That is 6.32 volts here. The increased voltage across the capacitor is resisting the current flow and reducing it proportionally. While the voltage across the capacitor has increased by 63.2% the current through the circuit has decreased by 63.2%.

If we double the resistance it will take twice as long for the voltage across the capacitor to reach 63.2% of the source voltage. The same thing will happen if we double the capacitance. If you double them both it will take four times as long for the capacitor to reach 63.2% or the source voltage. The above circuit has a time constant of 1 second. Double the resistance or the capacitance and the time constant will become 2 seconds. Double both the resistance and capacitance and the time constant will become 4 seconds.  We'll come back to that later. For now let's get back to the demonstration circuit.

We start with 10 volts at the battery and have 6.32 volts across the capacitor. Where are the rest of the volts? Remember Kirchhoff's Voltage Law. The voltages in a series circuit must add up to the battery voltage. With 6.32 volts across the capacitor the remaining 3.68 volts must be across the resistor.

After one time constant the capacitor has 6.32 volts and the resistor has 3.68 volts. This adds up to the battery voltage of 10 volts, satisfying Kirchhoff's Voltage Law.

Since this is a series circuit, whatever current is flowing through the resistor is flowing through the rest of the circuit. What is that current? We have 3.68 volts across 1 ohm. We know the voltage so we divide into it. 3.68  1 = 3.68 for 3.68 amperes. This is the current we measure anywhere in this series circuit. If time is frozen this circuit obeys all the rules we expect for DC circuits.

Now let's move forward to two time constants.

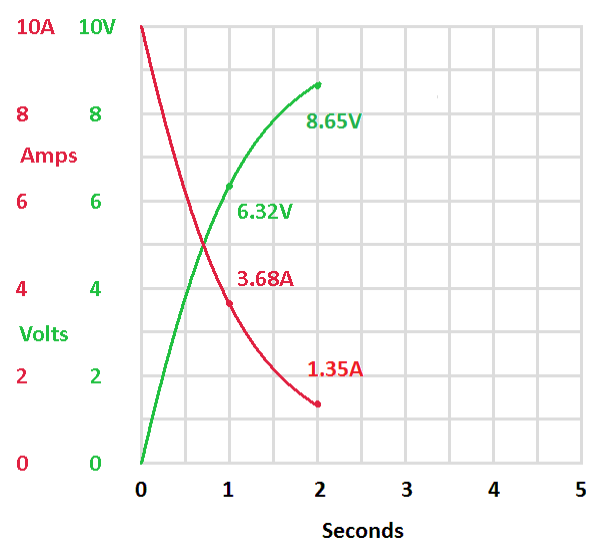The situation after two time constants (two seconds with this circuit).

Now the voltage across the capacitor is 8.65 volts. This is 63.2% of the difference between 6.32 volts and 10 volts. In the time from the first time constant to the second time constant the capacitor charged 63.2% of the remaining voltage. This happens for every time constant, the voltage across the capacitor increases by 63.2% of the remaining source voltage. The current follows the opposite course. For each time constant the current decreases by 63.2% of the remaining value.

Now let's see what happens after five time constants.

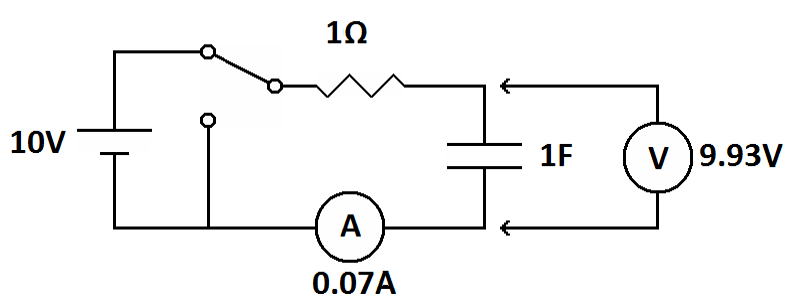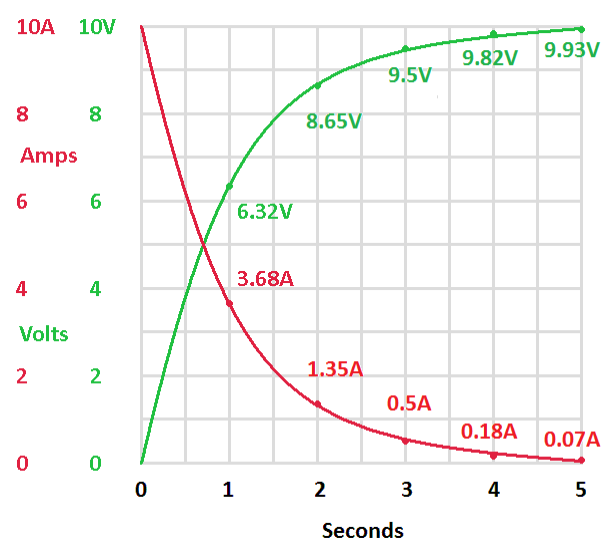After five time constants the voltage has essentially reached the source voltage and the current has reached zero.

Now, at 99.3% of the source voltage the capacitor is essentially fully charged. In reality the voltage will never reach the source voltage. It will just get closer and closer. However, the voltage is now only 0.7% away from the battery voltage. It's fully charged. Let's move on.

Capacitors as DC blockers

After five time constants the current has essentially reached zero amps. When the capacitor first started charging there was a rush of current but after five time constants it has stopped (or at least is very low). When you apply a DC voltage to a capacitor you will get a surge of current then the capacitor quickly blocks current flow. The capacitor is now essentially what it says on the box, two conductors separated by an insulator. It's an open circuit. All the source voltage appears across the open circuit and there is no current flow (see Open circuits above). This is why capacitors are said to block DC but pass AC. As long as the voltage remains constant, they do.

However, the capacitor has something that any plain old open circuit does not have. It has an energy store. This energy can be released to do work. A charged capacitor is a lot like a battery but doesn't have anywhere near the energy density of a battery. It's like comparing a compressed air tank to an air compressor. The compressor will supply compressed air as long as you supply power to it. A compressed air tank will quickly run out of air. We will see how this energy store is used in practical circuits when we study practical circuits in another volume.

Demonstration:

You can watch a capacitor as an energy store in action using an analog multimeter. Put the meter in the ohms range and place the probes across a large capacitor (1,000 microfarads or so). When in the ohms range the red probe may or may not be positive. You may have to try it both ways. You should see a very low resistance at first but as the capacitor charges the resistance will increase eventually reaching infinity. Now put the meter in a low voltage range and place it across the capacitor. You should see some voltage. How much depends on the battery used by the meter to measure resistance. This voltage should go down slowly as the capacitor discharges.

Now let's change the resistance to 2 ohms and see what happens to the time constant. Start by discharging the capacitor. Now flip the switch to the charge position and freeze time when the voltage reaches 6.32 volts.

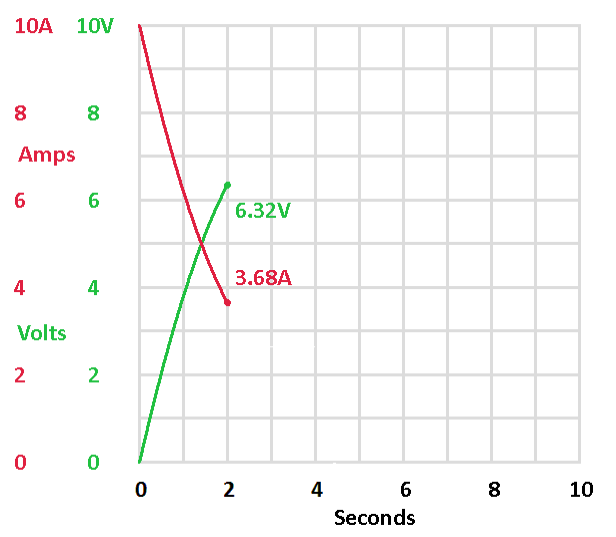Same circuit with a 2 ohm resistor. Notice that it takes twice as long for the capacitor to reach 63.2%		This is the same circuit as to the left. Here the horizontal scale has been shrunk in half. Notice that the shape of the curves is identical to the original 5-second scale.

This time it took two seconds to reach 63.2% of the battery voltage. What happened. It's like pinching the hose from the air compressor to the air tank. The higher resistance caused it to take longer to fill the tank. The higher resistance does the same thing to the circuit. Twice the resistance leads to twice the time. Now put the 1 ohm resistor back in the circuit and change the capacitor to a 2 farad capacitor. We get exactly the same result. The time constant has increased to 2 seconds. Using the original horizontal scale on the graph the curve becomes stretched out. However, if we shrink the horizontal scale proportionally the curve looks identical to the original.

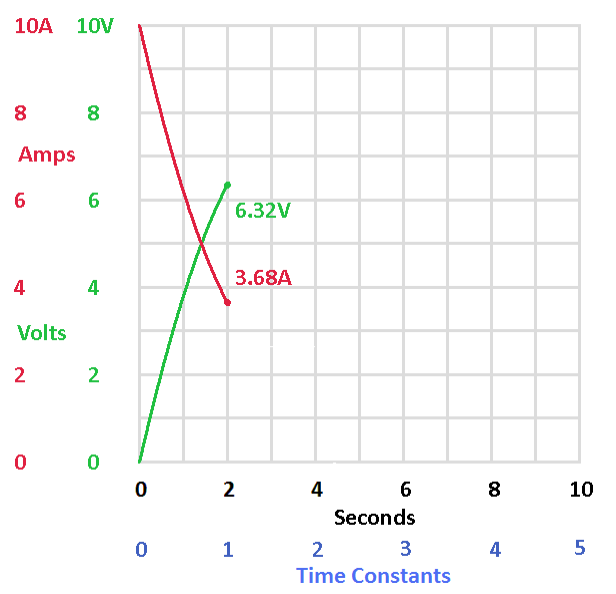
Let's change the scale so that it always shows 5 time constants, regardless of how long a time constant is.

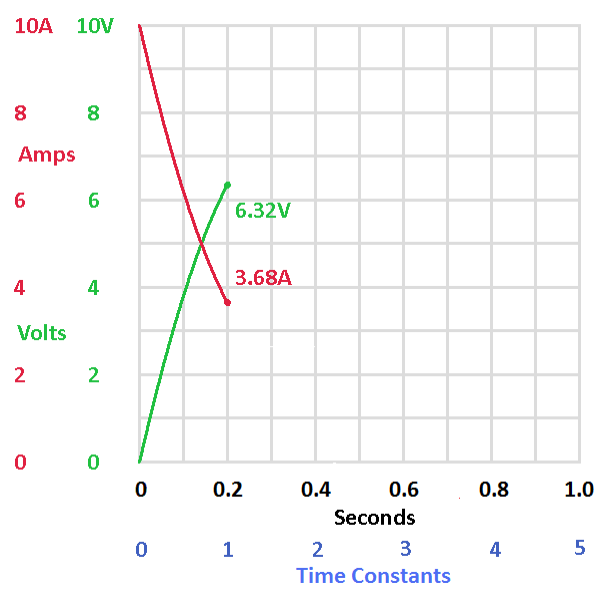Here we have 2 ohms and 1 farad. The time constant is 2 seconds.		Here we have 2 ohms and 100,000 microfarads. The smaller capacitor charges 10 times as fast so the time constant is only 200 mS (0.2 seconds). However, no matter how long a time constant is, the curves look identical if the horizontal scale is in time constants.