Exercise, Ohm's law and Kirchhoff's law practice:

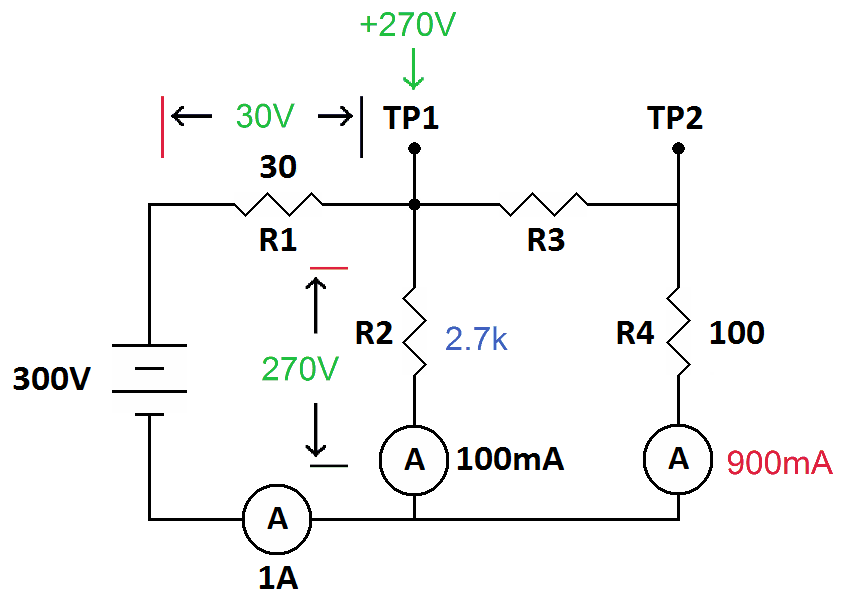
Now it's time to take a break and do another Ohm's law and Kirchhoff's law practice circuit. For the following circuit find: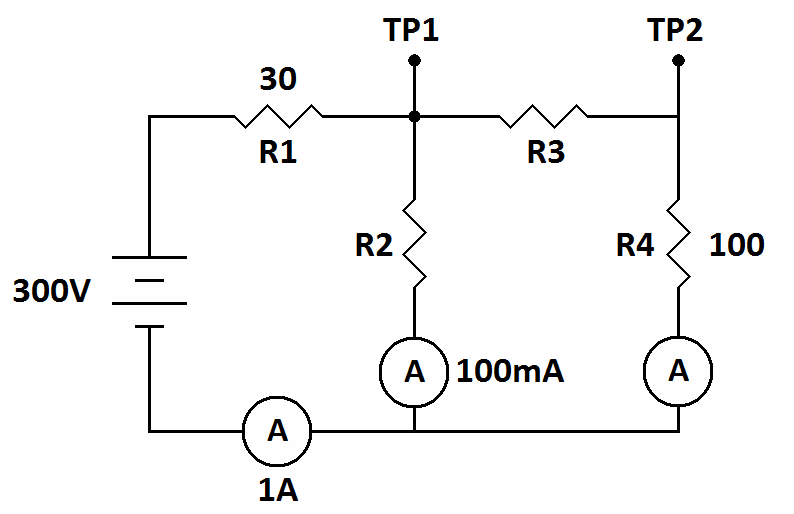


Find:


Note that there is no omega (Ω) after the resistor values. You will not always see the omega in real schematics so I have left them out here.

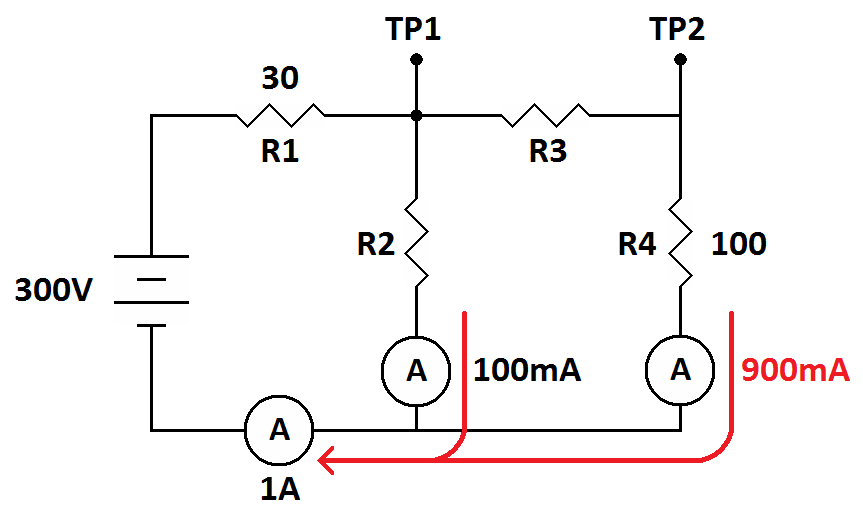
Start out the same way you did the first problem. Find something you don't know that you have enough information to calculate. One stand-out is the current through R4 (the unlabeled current meter). The total current in the circuit is 1 amp. There are two legs in the parallel part of the circuit and one leg has 100mA flowing through it. The rest of the total current must be flowing through the other leg (Kirchhoff's Current Law). The unknown current must be 900mA.


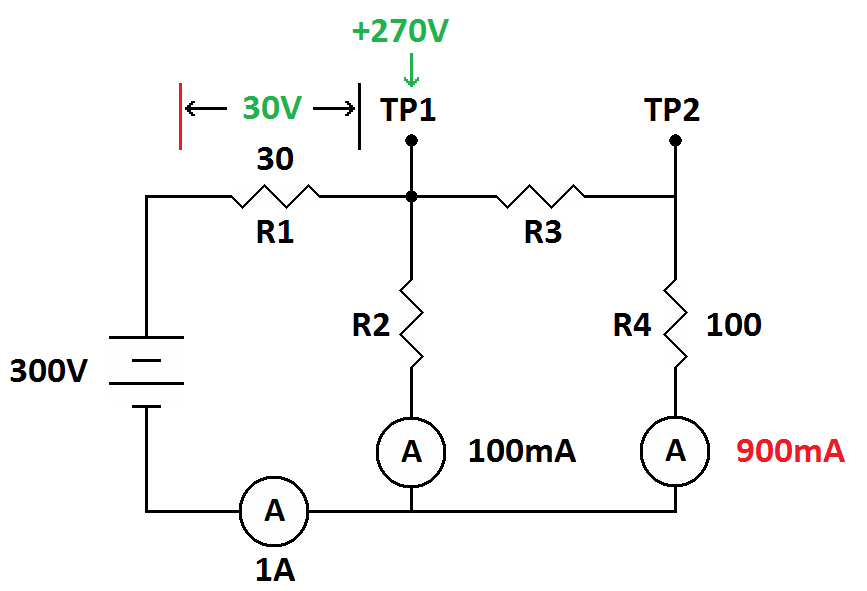
An equal stand-out is R1. The battery and R1 constitute a series circuit (only one current path) so the current shown on the bottom leg is the same current flowing through R1 (you didn't divide 300 volts by 30 ohms did you? Shame on you). There we have 30 ohms and 1 amp. Since we don't know the voltage we multiply. That's 30 ohms times 1 ampere. On the calculator that is...

3

0

X

1

=

30

 ...for 30 volts. We will assume that ground is the negative side of the battery so that is our zero volt reference. We will get +300 volts at the positive side of the battery and drop 30 volts across R1 leaving 270 volts at TP1.


Now we have enough information to calculate the value of R2. The entire bottom leg of the circuit is zero volts. Remember that a current meter is a short circuit so there is no voltage differential across one.


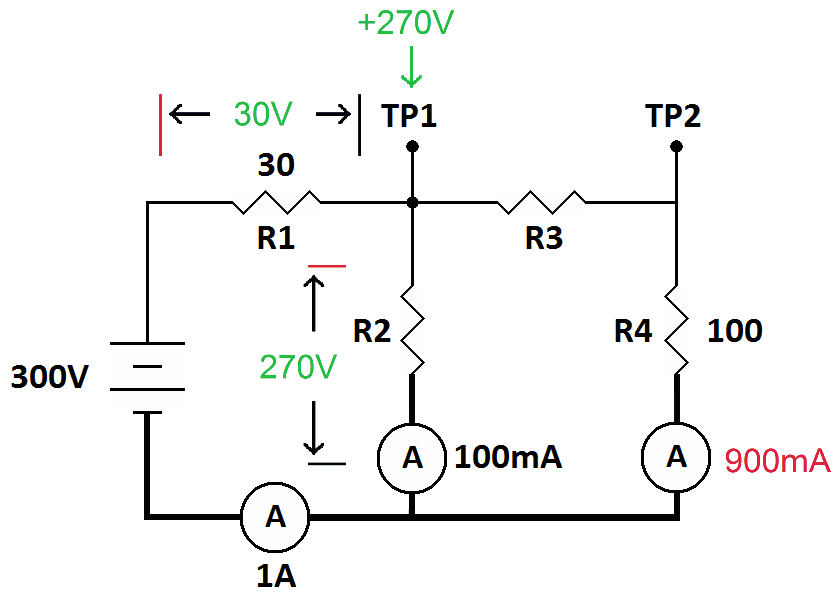
With 0 volts on one side of R2 and 270 volts on the other, the voltage across R2 is 270 volts. Knowing that there are 100 mA flowing through R2 there is enough information to calculate its value. Since we know the voltage we divide into it (converting 100mA to 0.1A). On the calculator that is...

2

7

0

.

1

=

2,700

...for 2,700 ohms or 2.7k.


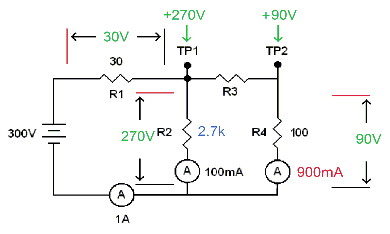
Next we will calculate the voltage at TP2 (could have done that sooner, actually). We have a 100 ohm resistor with 900 mA flowing through it. On the calculator that is...

.

9

X

1

0

0

=

90

...for 90 volts. R4 has 0 volts on the bottom side. Add this 90 volts and you have +90 volts at TP2

Now with the voltage at TP1 and the voltage at TP2 we can calculate the voltage across R3 using the basic series circuits rules. If TP1 is +270 volts and TP2 is +90 volts there is a 180 volt drop across R3. R3 is in series with R4 and the current meter. The current of 900mA is passing through R3. Now we can calculate R3's value. That's 180 volts 900 mA. On the calculator that is...

1

8

0

.

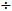
9

=

200

...for 200 ohms.

Solution: