| Vocademy |
R/L time constants
An RL circuit has a time constant much like an RC circuit. In this case the time constant is calculated by dividing the inductance by the resistance.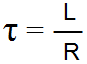
Where:
τ = time constant in seconds
R = resistance in ohms
L = inductance in henrys
R = resistance in ohms
L = inductance in henrys
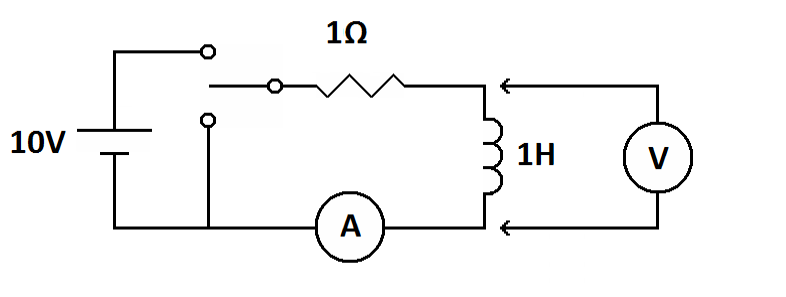
An inductor demonstration circuit
This circuit consists of a 10 volt battery, a 1 ohm resistor and a 1 henry inductor. Now let's flip the switch to the “charge” position and freeze time.
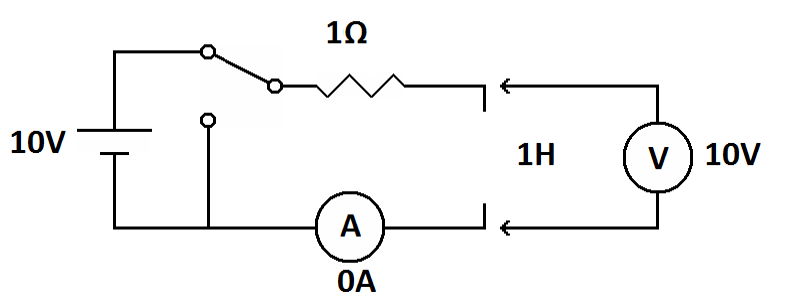
| At the moment the switch is moved to the “charge” position the inductor looks like an open circuit. |
At the moment the switch is flipped current rushes into the inductor. The building magnetic field pushes back and blocks the current flow. The inductor acts like an open circuit. Notice that the entire battery voltage is across the inductor (see Open circuits above). This is opposite to the capacitor, which acts like a short circuit at this point in time.
Now let's move time ahead. As the magnetic field builds it begins to slow down. This reduces the back EMF and current starts to flow in the circuit.
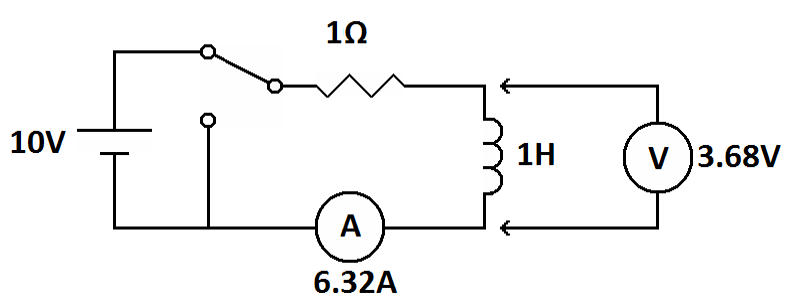
The circuit after 1 second
After 1 second the the voltage across the inductor has dropped by 63.2% and the current has increased proportionally. Now let's continue to 5 seconds.
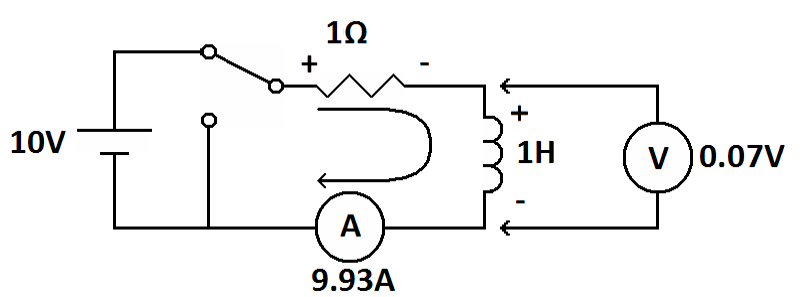
| After 5 seconds the inductor is essentially a short circuit. |
After 5 seconds the magnetic field is about as strong as its going to get. It is no longer moving so it no longer offers opposition to current flow. The inductor is now what it says on the tin. It's a piece of wire, essentially a short circuit. This demonstrates that an inductor acts opposite to a capacitor under the same conditions. The following chart lists those conditions and how a capacitor and inductor react to them.
| Event | The Capacitor | The Inductor |
| The switch is first closed | Looks like a short circuit | Looks like an open circuit |
| After one time constant | Voltage is 63.2% of source voltage | Current is 63.2% of maximum |
| After several time constants | Voltage is at maximum (equal to source voltage) |
Current is at maximum |
| The switch is moved to discharge position |
Current reverses direction | Voltage reverses across inductor |
| After one time constant | Voltage is 36.8% of source voltage | Current at 36.8% of maximum |
| After several time constants | Current and voltage are at 0 | Current and voltage are at 0 |
In reality the bulk of wire that the inductor is made from has some resistance. Inductors made of many turns of fine wire have significant resistance. Because of this an inductor can be represented by a coil of wire in series with a resistor. Because of this resistance the inductor may not act like a dead short as demonstrated. An inductor made from a few turns of heavy wire certainly will, but one made of many turns of fine wire will have a lot of inherent resistance.
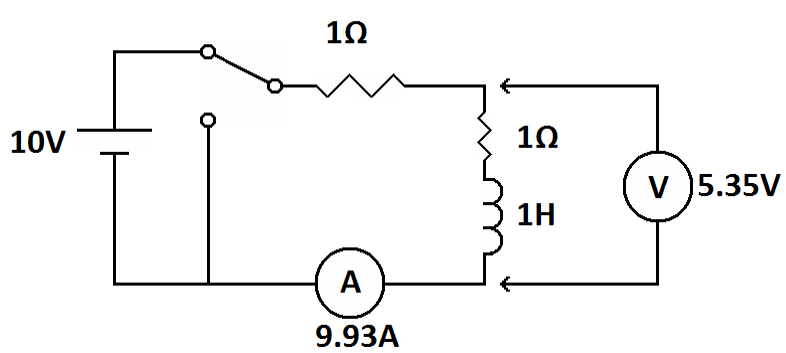
| An inductor made of many turns of fine wire will act like an inductor with a resistor in series. If the inductor has 1 ohm of inherent resistance, the circuit will be like this after 5 time constants. |
If that inherent resistance is 1 ohm, that will increase the circuit resistance to 2 ohms. That will make the time constant ½ second instead of one second. However, that just means that things happen faster. On the other hand, the voltage in the circuit gets distributed a little differently. After 5 time constants there is 0.07 volts across the inductor and 9.93 volts across both resistors. Since the resistors are equal that puts 4.965 volts across each resistor. The inherent resistance in the inductor is manifested in series with the inductor so its 4.965 volts is added to the inductor's 0.07 volts for a total of 5.035 volts. Therefore, the inductor will have 5.035 volts across it instead of 0.07 volts.

| After 5 seconds the current is flowing in the direction of the arrow and the voltage polarities are as shown (we are again assuming that the inductor has no inherent resistance). |
While the switch is in the “charge” position the resistor and inductor are acting as impedances. Therefore the voltage is positive where the conventional current enters the devices. After 5 seconds the inductor is essentially a short circuit. However, unlike any old short circuit the inductor has energy stored in its magnetic field. Under equivalent conditions a 1 henry inductor will store the same amount of energy in its magnetic field as a 1 farad capacitor will store in its electrostatic field.
Now let's flip that switch. When the battery is taken out of the circuit it no longer is pushing current through the inductor. Without this impetus the magnetic field begins to collapse. While the magnetic field was building it induced back EMF that pushed against the current from the battery. While it is collapsing the magnetic field is moving in the opposite direction. Therefore the current it induces is in the same direction that the current is already flowing. Without the battery pushing it the current wants to stop instantly. However, the collapsing magnetic field keeps it going.
At this point the inductor becomes a current source. Remember that a current source is positive where conventional current exits. While the circuit is in “charge” mode the inductor is an impedance so the the positive voltage is where the current enters. When we flip the switch the inductor becomes a current source. With the current continuing in the same direction, the voltage across the inductor flips. Look at the circuit above and see that the positive voltage is at the top of the inductor. Now let's look at the circuit at the moment we flip the switch.
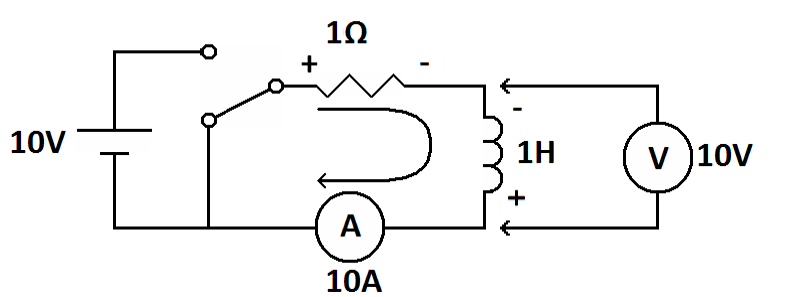
| At the moment the switch is flipped the inductor becomes a current source and its polarity flips. |
With the switch in the “discharge” position the current continues to flow with the inductor acting like a battery. As the magnetic field collapses the voltage across the inductor drops as does the current until the field is completely collapsed and we are back where we started. Here is the time constant graph relabeled for the inductor demonstration circuit.
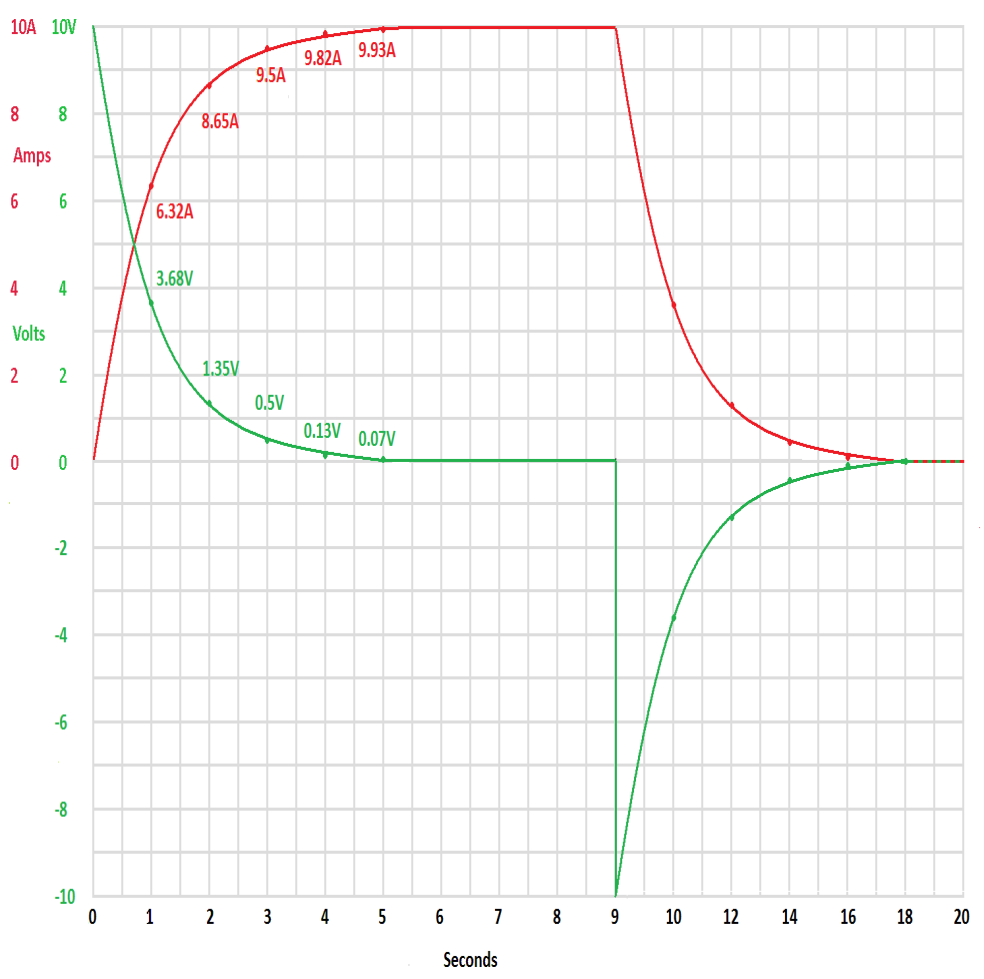
| The time constant curve for the inductor circuit. Green is voltage across the inductor and red is current through the circuit. This graph is exactly opposite to the capacitor graph. |
The graph is identical to the capacitor graph except the voltage across the inductor acts like the current through the capacitor and vice versa. Notice the sudden flip in the voltage polarity across the inductor when the switch is flipped.
| Vocademy |
