Signal gain with BJTs is simpler than with FETs, so we will cover
that first. When a small current is sent into the base of a bi-polar
junction transistor a larger
current flows into the collector. The question is how
much larger. In a BJT the ratio of the base
current compared to the collector is called hFE[1].
Notice
that the "h" is lowercase
and the "FE" is uppercase. This means that the parameter is for DC
operation. For AC operation the equivalent parameter is called hfe
(lowercase "fe").
hFE is the ratio of collector current to base current:
hFE
=
IC
—————
IB
Where:
hFE
=
Collector current to base
current ratio.
IC
=
Collector current, current
flowing into the collector
IB
=
Base current, current flowing
into the base
This formula means that to find the collector current, multiply the
base current by hFE.
IC = hFEIB
For example, if an NPN transistor has an hFE of 50
and 1 mA of current
flows into the base, 50 mA will flow into the collector.
The
collector current of a BJT has a fairly linear relationship to the base
current. If we change the base current by a certain percentage the
collector current will change by about the same percentage[2].
For this
reason Bi-polar
junction transistors are said to be current controlled or to amplify
current.
The hFE is not an absolute value. It differs depending on
the collector
current and the collector-to-emitter voltage. A data sheet for a
particular transistor will list several values for hFE, each
for a
different collector current and collector-to-emitter voltage
combination.
The AC equivalent of hFE, called hfe. On
transistor datasheets it is usually listed under the title of "Small
Signal Gain". This the
ratio of the change
in collector current to the change in base current. Here is the formula
that defines hfe:
hfe
=
ΔIC
—————
ΔIB
Where:
hfe
=
Ratio of change in collector
current to change in base current
ΔIC
=
Change in collector current
(delta IC)
ΔIB
=
Change in base current (delta IB)
Where hFE tells us how much collector current we will get
with a certain base current, hfe tells us how much the
collector current will change
if we make a change in the base current.
ΔIC = hfeΔIB
For example, if an NPN transistor has an hFE of 50,
and 2 mA of current
flows into the base, 100 mA will flow into the collector. If we
increase the base current to 3 mA we get a collector current of 150 mA.
We increased the base current by 1 mA and the collector current
increased by 50 mA. Therefore, this transistor not only has an hFE
of 50 but also has an hfe of 50. The values of hFE
and hfe are usually pretty close to each other. However,
because hFE is different for different amounts of collector
current, hfe will differ slightly from hFE.
Beta
Sometimes the ratio of collector current to base current is
called beta (β). However, this is not an industry standard and
literature is inconsistent on the definition. Most sources say that
beta is identical to hFE. Some say that
beta is the AC gain and
that hFE is the DC gain. Transistor data sheets typically
avoid using
the term "beta" and strictly use hFE to describe DC gain and
hfe to
describe AC gain.
Alpha
Alpha (α) is another parameter you may come across.
Alpha is
the ratio of the emitter current to the collector current. Notice in
the diagram above that the current that flows into the base flows out
the emitter along with the collector current; the emitter current is
the sum of the collector current plus the base current (recall
Kirchhoff's Current Law). The base
current is usually quite small compared to the collector current, so
alpha is typically a small value. Alpha is useful when working with
common-base amplifiers (discussed in Analog Circuits).
Darlington pairs
Frequently, super-high current gains are required with BJTs. For
example, a power transistor may require 100 mA of base current to
deliver 5 amps of collector current (where the hFE is 50).
However, the
circuit "driving" the transistor may be only able to deliver 50
mA. The answer to this problem is a darlington pair.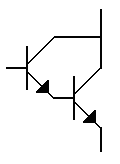
Schematic symbol for an NPN
Darlington pair
In a darlington
pair, the emitter of a low-power transistor feeds the base of a
high-power transistor. In the above case, the 50 mA available from the
driving circuit is more than enough to cause the low-power transistor
to deliver 100 mA to the base of the power transistor. Darlington pairs
can be made from any pair of BJTs. You can also obtain Darlington pairs manufactured together
in a single package.
To find the gain of a darlington pair multiply the hFE of the two transistors together. If the low-power transistor has an hFE of 100 and the high-power transistor has an hFE of 50, together they have an "hFE" of 5,000.
FETs
The signal gain of an FET is a bit more complicated than with a BJT.
The gate current is very small (practically nonexistent with MOSFETs) and the relationship of gate current to
drain current is nonlinear. However, the relationship of gate voltage
to drain current is fairly linear under certain parameters. For this reason FETs are said to be voltage controlled or
that they amplify voltage.
The equivalent of hFE is called transconductance and is defined as
follows:
gm
=
ID
—————
VGS
Where:
gm
=
Transconductance—ratio of drain current to gate
voltage
ID
=
Drain current
VGS
=
Voltage between the gate and the
source.
However, this relationship isn't as simple as the relationship of base
current to collector current in BJTs. First of all, with J-FETs and
depletion mode MOSFETs, the relationship is
inverse; as gait voltage goes up, drain current goes down. Also, a
voltage of several volts may result in a current of several milliamps.
You can't compare voltage to current that way (apples to oranges), it appears to be a
loss rather than a gain. However, you can design a circuit such
that a small change in the gate voltage causes a larger change in the
drain-to-source voltage (VDS). This will be covered briefly
in Transistor Characteristics.
